Vector Multiplication (Inner Product & Cross Product)
A vector has a "magnitude" and a "direction". We already know how to multiply a "magnitude" with another "magnitude". Herein, I intend to explain how to multiply a "vector" and another "vector". (If you want to know how to multiply a "vector" with a "scalar" please refer to the "scalar and vector” page.)There are two types of vector multiplication: "inner product" and "cross product". Herein, both types of multiplication will be described in detail. Finally, the difference between "inner product" and "cross product" will be also defined.
Inner Product
The inner product of vectors is defined as the value obtained by multiplying the magnitudes of two vectors and the cosine of the angle \(\theta\) formed between the two vectors. \begin{eqnarray} {\bf A} \cdot {\bf B} = |{\bf A}||{\bf B}| \cos \theta \end{eqnarray} To express the inner product, we must use "\(\cdot\)". The component of the inner product is expressed as follows: \begin{eqnarray} {\bf A} \cdot {\bf B} = A_x B_x + A_y B_y + A_z + B_z \end{eqnarray} When the angle between the two vectors is 90°, the inner product is always equal to 0. By the way, what does inner product mean? The answer is “work”. For the sake of clarity, we consider a case where an object is inclined from the horizontal plan with an angle \(\theta\) in the upward direction, as shown in Figure 1 and pulled by a force \(F\) with a distance \(d\). \begin{eqnarray} W = {\bf F} \cdot {\bf d} = |{\bf F}||{\bf d}| \cos \theta \end{eqnarray} When the angle between the two vectors is 90°, the inner product (\(W\)) is equal to 0. This is called an orthogonal condition of vector. As the inner product of a vector is a scalar, it is also called the “scalar product”. Herein, I intend to describe the basic properties of the inner product (exchange rule, distribution rule, etc.). \begin{eqnarray} {\bf A} \cdot {\bf B} &=& {\bf B} \cdot {\bf A}\\ {\bf A} \cdot ( {\bf B} + {\bf C} ) &=& {\bf A} \cdot {\bf B} + {\bf A} \cdot {\bf C} \\ a ({\bf A} \cdot {\bf B} ) &=& (a {\bf A} ) \cdot {\bf B} = {\bf A} \cdot (a {\bf B} ) \end{eqnarray}
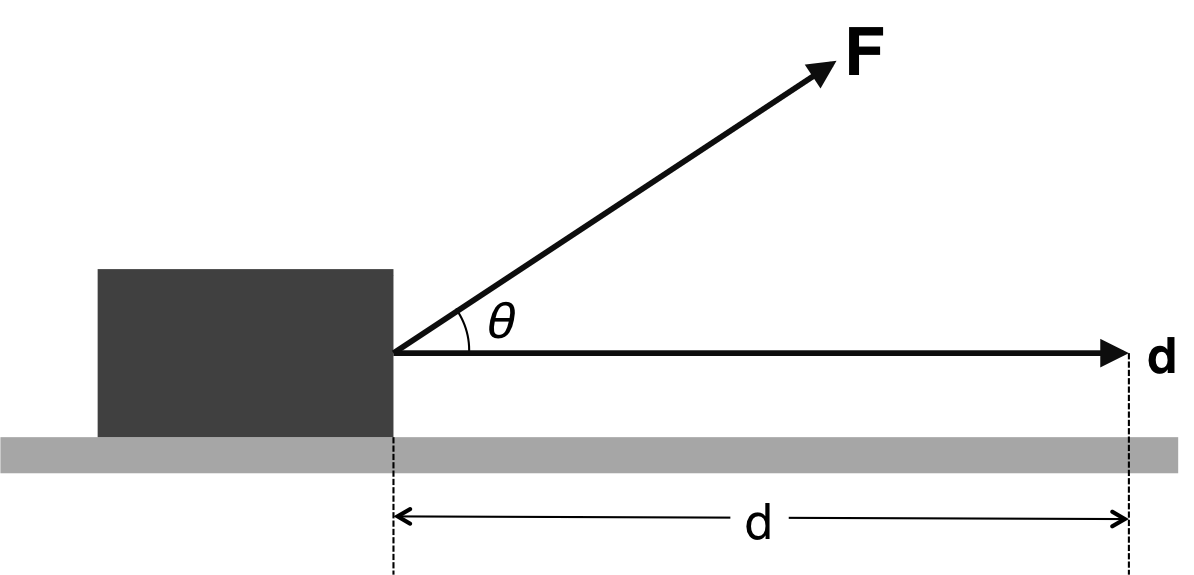
Figure 1. Schematic representation of the work
Cross Product
The cross product C of a vector \({\bf A}\) and a vector \({\bf B}\) is defined as follows: \begin{eqnarray} {\bf C} = {\bf A} \times {\bf B} = | {\bf A} | | {\bf B} | \sin \theta {\bf \hat{C}} \end{eqnarray} \( \hat{C}\) is a unit vector having the same direction as. The cross product of two vectors is a vector. Therefore, the cross product is also called the “vector product”. The length of \({\bf C}\) corresponds to the area of the parallelogram (Gray shade) formed by the vector \({\bf A}\) and vector \({\bf B}\), as illustrated in Figure 2. The direction of \({\bf C}\) is perpendicular to the plane (the parallelogram) created by the vector \({\bf A}\) and the vector \({\bf B}\). The direction according to the right hand screw rule (right hand system) is the direction of the vector \({\bf C}\) (see Figure 2). In physics, this rule is mainly used to represent a torque and Lorenz’s force.
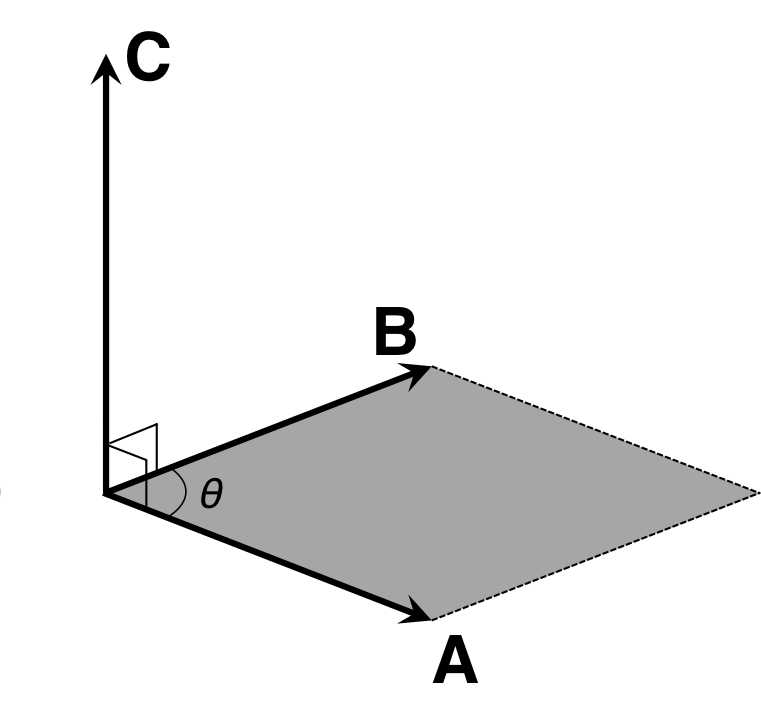
Figure 2. Schematic illustration of the cross product
In the case of the inner product, the exchange rule applies. However, in the case of the cross product, the exchange rule does not apply, as follows: \begin{eqnarray} {\bf A} \times {\bf B} \ne {\bf B} \times {\bf A} \end{eqnarray} Finally, we wrote the fundamental rules for the cross product as follows: \begin{eqnarray} {\bf A} \times {\bf B} &=& - {\bf B} \times {\bf A}\\ {\bf A} \times ( {\bf B} + {\bf C} ) &=& {\bf A} \times {\bf B} + {\bf A} \times {\bf C} \\ (a{\bf A}) \times {\bf B} &=& {\bf A} \times (a {\bf B} ) \end{eqnarray}
Sponsored link