スカラーポテンシャル
例えばベクトル場\( {\bf A} \)があるとする。
そのベクトル場はそれぞれの点における傾きで表せるとするとベクトル場\( {\bf A} \)は
\begin{equation}
{\bf A} = - \nabla \phi \ \ \ \ \ \ \ \ \ \ \ (3.16.1)
\end{equation}
と表される。本来なら\( \nabla \)の前に負の符号を付けるか付けないかはあまり関係ないが、物理の場面では負の符号を付けるのが通例なので、ここでもそれに従う。
このとき\( \phi \)をベクトル場\( {\bf A} \)のスカラーポテンシャルと呼ぶ。
スカラーポテンシャルとはどういうものなのだろうか?
高校物理の知識だと位置エネルギーをポテンシャルエネルギーと呼ぶこともあった。
そこからも想像できるように、ポテンシャルとはあるスカラー物理量の「大きさ」を意味する。
ここでは一番想像しやすい「高度」で考える。
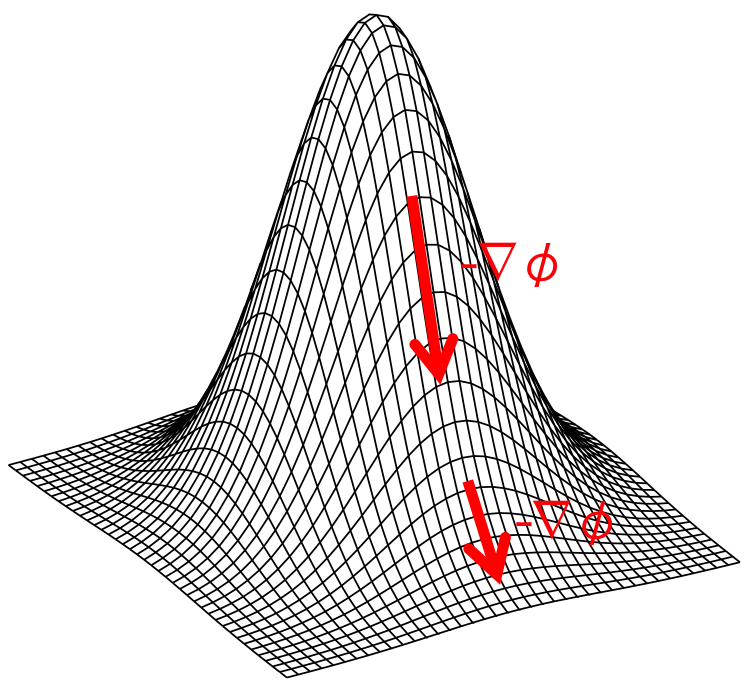
図3-16-1 ベクトル場とスカラーポテンシャルの関係。各点での高度がスカラーポテンシャルで赤いベクトルが\( - \nabla \phi \)に相当する。
図3-16-1に簡単な山を示した。山の高度はポテンシャル\( \phi \)に相当する。
山の頂上から麓(ふもと)まで高度は減っていく。つまり、ポテンシャルは減っていく。
\begin{equation}
{\bf A} = - \nabla \phi = - \left( \frac{\partial}{\partial x}\phi,\ \frac{\partial}{\partial y}\phi,\ \frac{\partial}{\partial z}\phi \right) \ \ \ \ \ \ \ \ \ \ \ (3.16.2)
\end{equation}
式(3.16.2)からもわかるようにもし、\( \phi\)の勾配だけをとった場合、そのベクトル(\( \nabla \phi \))の向きは図3-16-1の赤のベクトルと逆向きになる。
もっと砕けた言い方をすれば、\( \phi \)は高度が高くなる方向に向くのである。
しかし、例えば水をこの山に垂らすと高度が減る向きに流れる(赤のベクトルの向き)。
もっと物理的に考えると、ポテンシャルが小さい方が安定するので、ポテンシャルが小さい安定的な方向に水は向かっていく。
つまり、\( \nabla \phi \)でベクトル場を示してしまうと物理の法則と反対の向きになってしまうのである。
このことから物理ではベクトル場とスカラーポテンシャルの関係に負の符号を用いるのである。(と私は思っている。)
わかり易い例として、水の流れのベクトル場のスカラーポテンシャルを「高度」で表した。
他のわかり易い例は、電場のポテンシャル場のスカラーポテンシャルは「電位(ボルト)」であることが挙げられる。
広告
