ベクトル演算子(発散・div)
ベクトルの発散・divergenceは以下のように定義される。 \begin{eqnarray} \mathrm{div} {\bf A} = \nabla \cdot {\bf A} &=& \left( {\bf i}\frac{\partial}{\partial x} + {\bf j}\frac{\partial}{\partial y} + {\bf k}\frac{\partial}{\partial z} \right) \cdot \left( A_x{\bf i} + A_y{\bf j} + A_z{\bf k} \right) \\ &=& \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \end{eqnarray} 発散はベクトルとベクトルの内積であたえられるので、スカラー量となる。 この発散のもつ物理的意味を考える。 ベクトル場中の任意の点で発散を計算し、その値が正であった場合、その点からベクトルが流出していることを意味します。 反対に発散を計算したら負であった場合、その点にベクトルが流入していることを意味するのである。 では、発散が0であった場合はどうでしょう。 発散が0であった場合は、その点に流入するベクトルと流出するベクトルが釣り合っていることを意味します。 図3-23のようにイメージするとわかりやすい。
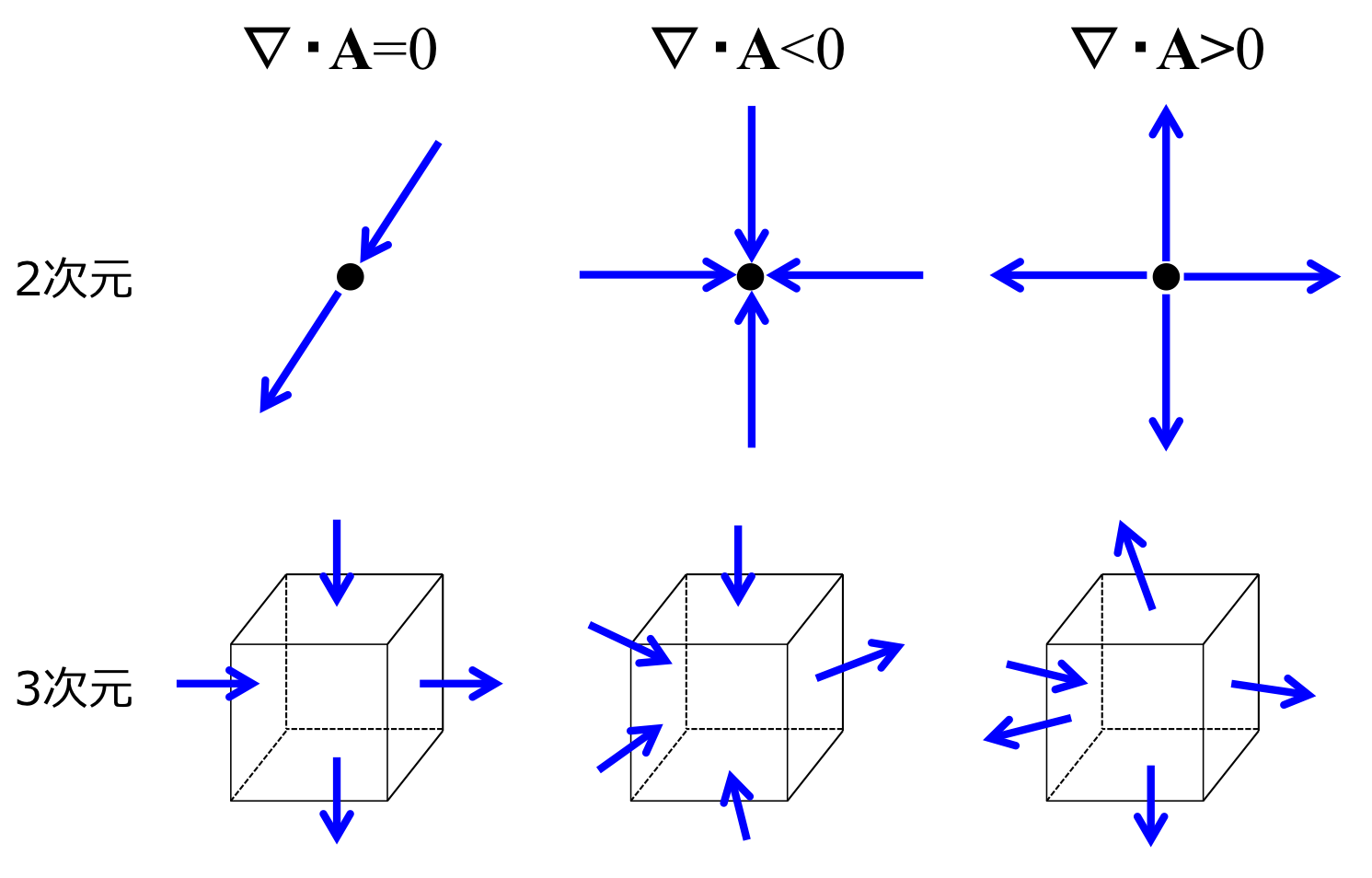
図3-23 発散のイメージ図。青の矢印でベクトルの流入を示す。
発散の数学的考察
ではなぜ、流入、流出ということがいえるのか。 次に、もっと数学的に発散の概念を考えていく。 水(非圧縮性の流体)が座標系中を速度\( {\bf v}(x,\ y,\ z) \)で流れているとする。 速度のx, y, z成分をそれぞれ、\( v_x(x,\ y,\ z),\ v_y(x,\ y,\ z),\ v_z(x,\ y,\ z) \)とする。 特に、Pでのそれぞれの速度を\( v_x,\ v_y,\ v_z \)とする。 一見、単位体積中に流れ込んだ水は出て行く水の量と変わらない気がするが、 これは単位体積中に蛇口と排水溝があると考えると、流入と流出が存在しても不思議でないことがわかる。 図3-24の様な直交座標系中の単位体積を考える。 x軸と垂直な面PQRS(灰色の面)に単位時間に流入する水は、Pの速度は、Pにおける\( {\bf v} \)の速度\( {\bf v_x} \)と 面PQRSの面積\( \Delta y \Delta z \)の積、\( v_x \Delta y \Delta z \)で表される。 ここで、その対面の面P’Q’R’S’での水の速度は点P’での速度で表され、\( v_x (x+\Delta x,\ y,\ z) \)である。
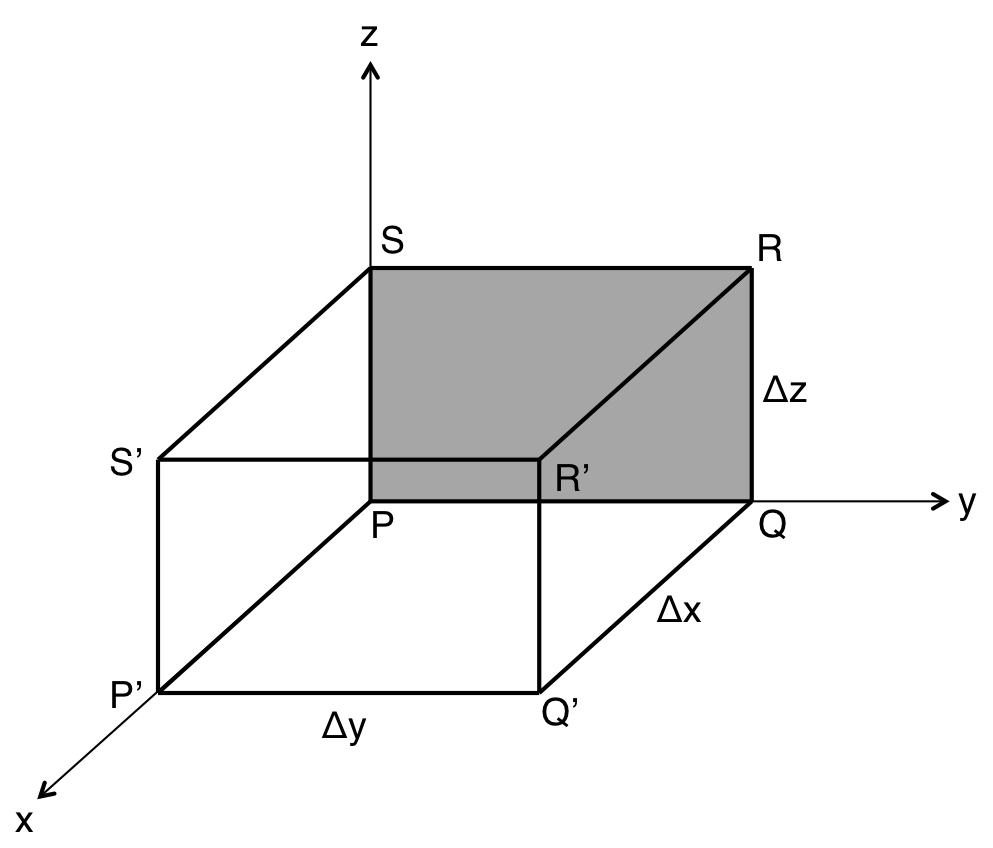
図3-24 直交座標系中の微小な正方形
この速度を式変形することで、 \begin{eqnarray} v_x (x+\Delta x,\ y,\ z) &=& v_x (x+\Delta x,\ y,\ z) - v_x + v_x \\ &=& \frac{v_x (x+\Delta x,\ y,\ z) - v_x }{\Delta x}\Delta x + v_x \\ &=& v_x + \frac{\partial v_x}{\partial x} \Delta x \end{eqnarray} よって、この単位体積内への流入量はそれぞれの差をとって、 \begin{equation} \left( v_x +\frac{\partial v_x}{\partial x}\Delta x \right) \Delta y \Delta z - v_x \Delta y \Delta z = \frac{\partial v_x}{\partial x} \Delta x \Delta y \Delta z \end{equation} と与えられる。左辺1項目が単位体積への流入量、2項目が流出量である。 これらと同じことが、y軸、z軸に垂直な面で起きる。よって、それぞれを足し合わせると、 \begin{eqnarray} \frac{\partial v_x}{\partial x} \Delta x \Delta y \Delta z + \frac{\partial v_y}{\partial y} \Delta x \Delta y \Delta z + \frac{\partial v_z}{\partial z} \Delta x \Delta y \Delta z &=& \left( \frac{\partial v_x}{\partial x} + \frac{\partial v_y}{\partial y} + \frac{\partial v_z}{\partial z}\right)\Delta x \Delta y \Delta z\\ &=& \left( \nabla \cdot {\bf v} \right)\Delta x \Delta y \Delta z \end{eqnarray} となる。\( \Delta x \Delta y \Delta z \)は単位体積を表すので、やはり、\( \Delta \cdot {\bf v} \)は単位時間に単位体積に流れ出る量(流出を正にしているので)を表すのである。