ベクトル演算子（勾配・grad）　　　

ナブラ演算子
ベクトルの偏微分\( \partial/\partial x,\ \partial/\partial y,\ \partial /\partial z \)は物理現象や特性を解き明かすのに非常に重要である。ここではベクトルを偏微分するのに便利（重要）なベクトル演算子であるナブラ演算子を紹介する。ナブラ演算子は \begin{equation} \nabla = {\bf i} \frac{\partial}{\partial x} +{\bf j} \frac{\partial}{\partial y} + {\bf k} \frac{\partial}{\partial z}\ \ \ \ \ (3.12.1) \end{equation} と記述される。演算子の”子”は”〜をするもの”という意味で、演算子は演算するものという意味である。ナブラ演算子はベクトルの「勾配・gradient」、「発散・divergence」、「回転・rotation」を記述するために用いられる。

勾配・gradient
スカラー関数\( \phi(x,\ y,\ z) \)の勾配（グラジアント、gradient）は \begin{eqnarray} \mathrm{grad} \phi &=& \nabla \phi = \left( {\bf i}\frac{\partial}{\partial x} + {\bf j}\frac{\partial}{\partial y} + {\bf k}\frac{\partial}{\partial z} \right) \phi \\ &=& \frac{\partial \phi}{\partial x}{\bf i} + \frac{\partial \phi}{\partial y}{\bf j} + \frac{\partial \phi}{\partial z}{\bf k} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3.12.2) \end{eqnarray} で定義される。では、この勾配は物理的にはどう意味があるのか考えていく。まず、\( {\bf r} = \sqrt{x^2 + y^2 + z^2}\)の勾配、\( \nabla {\bf r} \)を計算する。 \begin{eqnarray} \frac{\partial r}{\partial x} &=& \frac{\partial}{\partial x} \sqrt{x^2 + y^2 + z^2} = \frac{x}{\sqrt{x^2 + y^2 + z^2}} = \frac{x}{r} \\ \frac{\partial r}{\partial y} &=& \frac{y}{r}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3.12.3) \\ \frac{\partial r}{\partial z} &=& \frac{z}{r} \end{eqnarray} より、 \begin{equation} \nabla r = \frac{x}{r}{\bf i} + \frac{y}{r}{\bf j} + \frac{z}{r}{\bf k} = \frac{1}{r}(x{\bf i}+y{\bf j}+z{\bf k})=\frac{{\bf r}}{r}\ \ \ \ \ \ \ \ (3.12.4) \end{equation} と導かれることができる。これを使って、次に\( \nabla (1/r) \)を求める。 \begin{eqnarray} \frac{\partial}{\partial x}\left( \frac{1}{r} \right) &=& \frac{\partial r}{\partial x} \frac{\partial}{\partial r} \left( \frac{1}{r} \right) = - \frac{x}{r^3} \\ \frac{\partial}{\partial y}\left( \frac{1}{r} \right) &=& - \frac{y}{r^3}\ \ \ \ \ \ \ \ (3.12.5) \\ \frac{\partial}{\partial z}\left( \frac{1}{r} \right) &=& - \frac{z}{r^3} \end{eqnarray} であるから、 \begin{equation} \nabla \left( \frac{1}{r} \right) =-\frac{x}{r^3}{\bf i} -\frac{y}{r^3}{\bf j} -\frac{z}{r^3}{\bf k} = - \frac{{\bf r}}{r^3}\ \ \ \ \ \ \ \ (3.12.6) \end{equation} となる。
ここで、図3-22のように原点に電荷\(q\)が置かれている場合を考える。

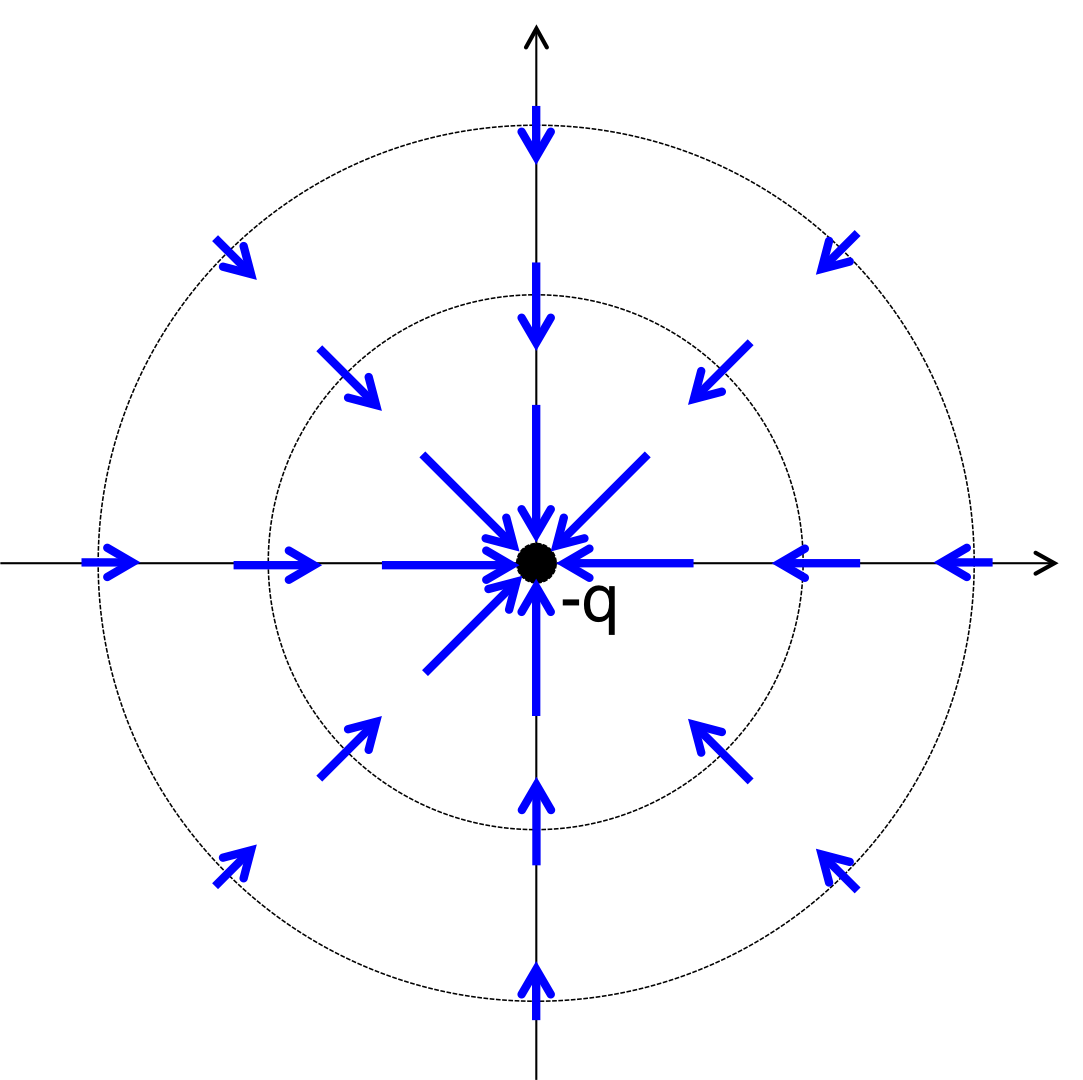
“fig22.png”
図3-22 原点に電荷qを置いた場合の等電位面（点線）と電場ベクトル（青矢印）。

電荷\(q\)による電場は、 \begin{equation} E = \frac{q}{4\pi \epsilon_0 r^2}\ \ \ \ \ \ \ \ (3.12.7) \end{equation} と表すことができる。電場はベクトル量であるので、電場をベクトルで表すと、 \begin{equation} E = \frac{q}{4\pi \epsilon_0 r^2} \frac{{\bf r}}{r} = \frac{q}{4\pi \epsilon_0} \frac{{\bf r}}{r^3}\ \ \ \ \ \ \ \ (3.12.8) \end{equation} と表すことができる。ここで、 \begin{equation} \phi = \frac{q}{4\pi \epsilon_0}\ \ \ \ \ \ \ \ (3.12.9) \end{equation} とすると、式(3.12.6)より、 \begin{equation} E = \nabla ( - \phi ) \ \ \ \ \ \ \ \ (3.12.10) \end{equation} となる。ここで、このように表される\( \phi \)をスカラーポテンシャルと呼ぶ。物理的に考えると、\( \phi \)は電位と呼ばれるので、ここでは便宜上\( \phi \)に負の記号を付けた。
ここまで、導出できたところで、この勾配と言う概念の物理的意味意味を考えていく。図3-22でも示したように、原点に電位を置くと、図3-22中の点線で示したように、等電位面が形成される。この座標系上の任意の点ではスカラーで与えられる電位\( \phi \)が計算できるので、この系はスカラー場である。原点に電荷-qが置かれたこの系で勾配を計算すると、青の矢印で示した電場ベクトルが形成される。注意してみると、この電場ベクトルは等電位面に垂直になることがわかる。もっと、わかりやすく例えると、山に等高線を引いて、そこに水滴を垂らすと、水滴は等高線に沿って、垂直に流れていくというイメージである。水滴の流れ落ちる方向が\( \nabla \phi \)の方向と一致する。
以上から言えることとして、スカラー場の勾配は任意の点において、そのスカラー量の変化が最大となる方向と大きさをもつベクトルを対応させるベクトル場になるということがわかる。