微分方程式を用いた解法（減衰振動）

図1. ばねにつながれた質点

図1のように、ばねにつながれた質点を考える。通常は床との摩擦は考えず、質点釣り合いの位置（\( x=0 \)）からずれると単振動を開始する。 ここではそうではなく、床と速度\( (v=\frac{dx}{dt}) \)に比例した運動方向と逆方向に働く摩擦力を考える。

この質点の運動方程式は、 \begin{eqnarray} m \frac{d^2x}{dt^2} = - kx - b\frac{dx}{dt}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} と書ける。ここで、\( m \)は質点の質量、\( k \)はばね定数、\( b \)は摩擦力の比例定数である。 式(1)は２階同次微分方程式である。

式(1)を整理すると、 \begin{eqnarray} \frac{d^2 x}{dt^2} + \frac{b}{m} \frac{dx}{dt} + \frac{k}{m} x = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} となる。式(2)の解が\( e^{\lambda t} \)の形になると仮定すると、特性方程式は \begin{eqnarray} \lambda^2 + \frac{b}{m} \lambda + \frac{k}{m} = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} となる。特性方程式を因数分解することを見越して、以下のように定数を定義する。 \begin{eqnarray} \gamma &=& \frac{b}{2m} \\ \omega &=& \sqrt{ \frac{k}{m} } \end{eqnarray} これを代入すると、 \begin{eqnarray} \lambda^2 + 2 \gamma \lambda + \omega^2 = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} となる。この方程式は簡単に解けて \begin{eqnarray} \lambda = - \gamma \pm \sqrt{\gamma^2 - \omega^2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} である。よって、２階同次微分方程式(2)の解は \begin{eqnarray} x &=& A e^{ \left(- \gamma + \sqrt{\gamma^2 - \omega^2} \right)t } + B e^{ \left(- \gamma - \sqrt{\gamma^2 - \omega^2} \right)t } \\ &=& e^{-\gamma t} \left\{ A e^{\sqrt{\gamma^2 - \omega^2}t} + Be^{-\sqrt{\gamma^2 - \omega^2}t} \right\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} である。ここで、\( A \)と\( B \)は定数である。式(6)は\( \gamma^2 - \omega^2 \)が正か負か、すなわち\(\gamma\)と\( \omega \)がどちらが大きいか、それとも互いに等しいかでその性質は大きく変わる。

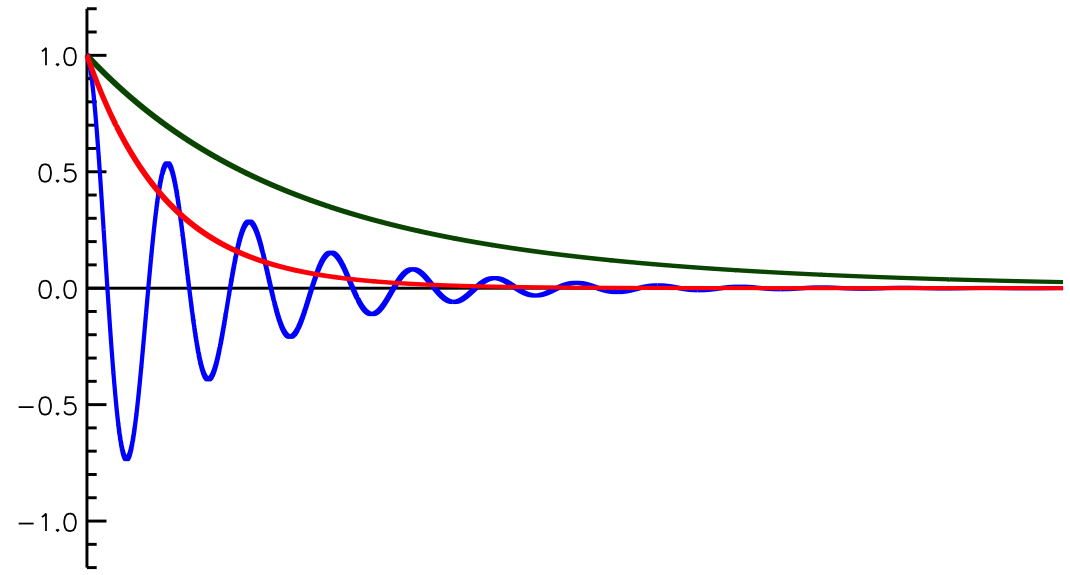
図2. 質点の位置の時間変化。(緑）過減衰、（青）減衰振動、（赤）臨界減衰。

\( \gamma > \omega \)の時（過減衰）

この時、\( \sqrt{\gamma^2 - \omega^2} \)が実数となる。つまり、\( x \)は、\( e^{-\gamma t} \)に従って0に収束していく。図2の緑線に相当する。この場合、振動することはない。

\( \gamma < \omega \)の時（減衰振動）

この時、\( \sqrt{\gamma^2 - \omega^2} \)は虚数となる。すると式(6)はオイラーの公式によって三角関数に展開できる。

ここで、\(C_1\)、\( C_2 \)は定数である。よりわかりやすくするために、三角関数の合成を使うと \begin{eqnarray} x = e^{-\gamma t} C_0 \sin \left( \sqrt{\omega^2 - \gamma^2}t + \phi \right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray} と表すことができる。ここで、\( C_0 = \sqrt{C_1^2 + C_2^2}\)、\( \tan \phi = \frac{C_2}{C_1} \)である。

式(8)が最も視覚的に分かり易い解である。つまり、図2の青線のように、この場合、質点は振動しながら、その振幅を\( e^{-\gamma t} \)に従って減衰させ、 釣り合いの位置\( x=0 \)に近づいていくのである。

\( \gamma = \omega \)の時（臨界減衰）

\( \gamma \)と\( \omega \)が等しい時、式(6)はシンプルになる。２階同次微分方程式の解き方を参考にして、 \begin{eqnarray} x = e^{-\gamma t} (A+Bt)\ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray} この時、質点は

臨界減衰