対数関数

対数関数とは以下のように表すことができる関数である。 \begin{equation} y = \log x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation} この時、底がネイピア数\( e = 2.71828 \cdots \)である対数を自然対数、底が10である対数を常用対数と呼ぶ。 多くの教科書などでは、自然対数を\( \ln \)、常用対数を\( \log \)で表す。 しかし、物理では自然対数を用いることが多いので、自然対数を\( \log \)とすることが多い。

対数関数で、 \begin{equation} y = \log_{10} x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{equation} と表せる場合、 \begin{equation} 10^{y} = x \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{equation} の関係がある。

これら２つの底をグラフにしたものが図1である。

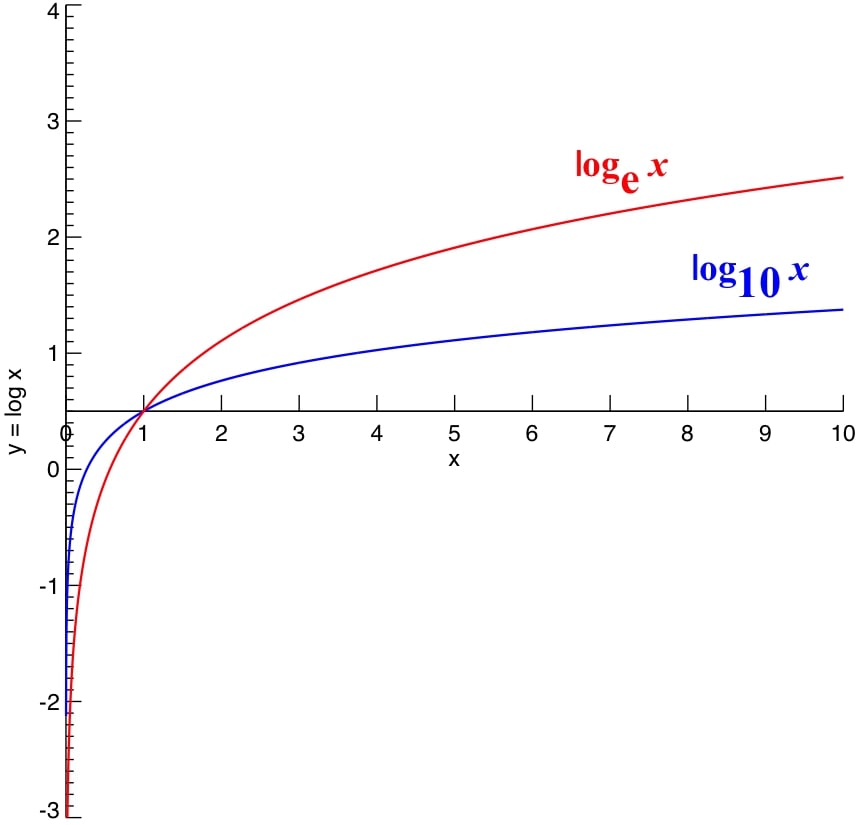
図1 自然対数と常用対数

対数関数の性質をまとめたものを以下に示す。これらの性質は自然対数でも常用対数でも同じで、底に依らない。 \begin{eqnarray} \log xy &=& \log x + \log y \\ \\ \log \left( \frac{x}{y} \right) &=& \log x - \log y \\ \\ \log_e e^x &=& x \\ \\ \log x^a &=& a \log x \\ \\ \frac{d}{dx} \log x &=& \frac{1}{x} \\ \\ \end{eqnarray}