指数関数

\( a \)を任意の定数として、 \begin{equation} y = a^x \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{equation} と表されるような関数を指数関数と呼ぶ。 物理数学では\( a \)をネイピア数である、\( e = 2.7182818284\cdots \)で表した、 \begin{equation} y = e^x \ \ \ \ \ \ \ \ \ \ \ (2) \end{equation} が重要な指数関数として用いられる。このような指数関数は以下のように微分してもその形が変わらない。 \begin{equation} y’ = e^x \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{equation} ネイピア数による指数関数は他の指数関数と同じ性質、 \begin{eqnarray} e^x \cdot e^y &=& e^{x+y} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \\ \frac{ e^x }{ e^y } &=& e^{x-y} \ \ \ \ \ \ \ \ \ \ \ \ (5) \\ \left( e^x \right)^y &=& e^{xy} \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} を持つ他に、以下に示す重要な性質も持つ。 \begin{eqnarray} e^x &=& 1 + x + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \cdots \ \ \ \ \ \ \ \ \ \ \ (7) \\ \frac{d}{dx} e^{ax} &=& a e^{ax} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (8) \\ \int e^{ax} dx &=& \frac{1}{a} e^{ax} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray} これらの特徴は物理の問題を解く際、特に微分方程式や積分を行う際に重要になる。

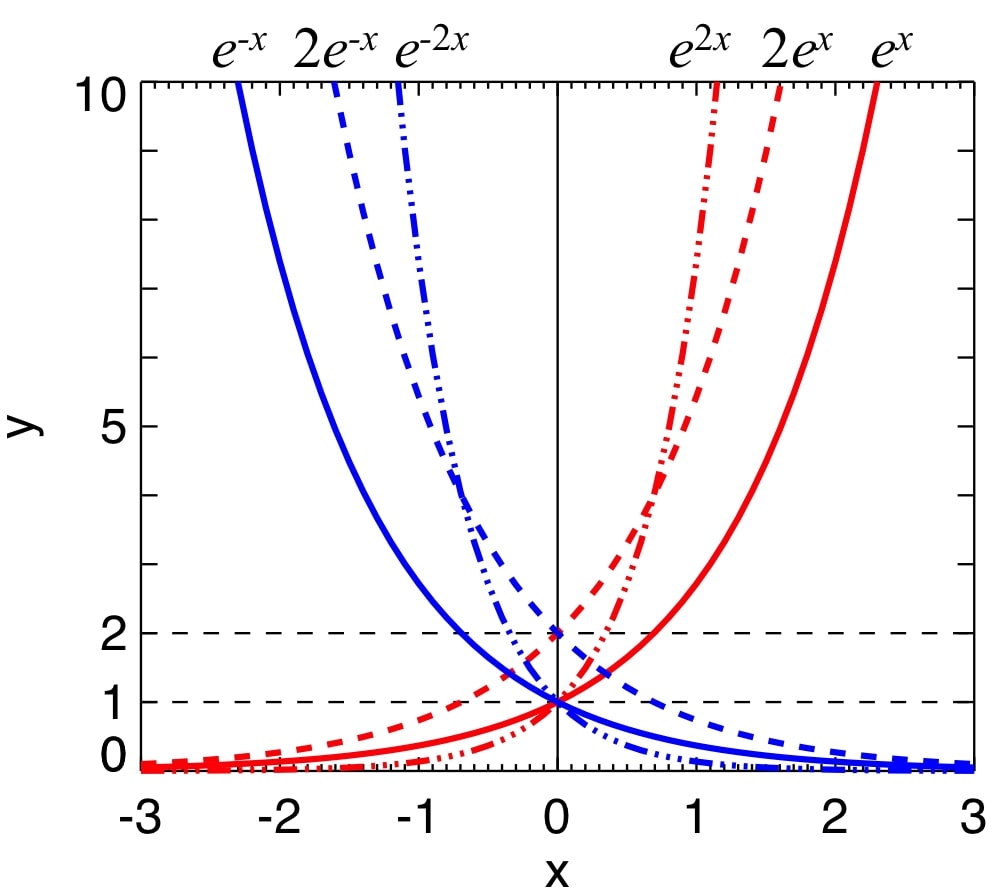
図1 指数関数

ここで紹介したネイピア数によって表される指数関数を座標に表したものを図1に示す。 指数関数と同様に対数関数も同時に学ぶと理解がスムーズである。