三角関数の合成
これまでは角度の足し算である加法定理、角度が異なる三角関数どうしの足し算、引き算である和積の公式、 異なる角度の三角関数どうしの掛け算である積和の公式を導いてきた。 これらの定理、公式は三角関数の係数が同じ場合に有効であった。
ここでは、異なる係数を持ち、同じ角度の三角関数どうしを足し合わせて一つの三角関数として表す
三角関数の合成
について説明する。 三角関数の合成は以下のように表される。 \begin{eqnarray} a\sin \theta + b \cos \theta = \sqrt{a^2 + b^2} \sin (\theta + \alpha)\ \ \ \ \ \ \ \ (1) \end{eqnarray} 三角関数の合成の方程式を証明していこうと思う。図1の様な2つの相似形の直角三角形を考える。 赤の三角形と青の三角形の斜辺の長さをそれぞれ、\( a \)、\( b \)とする。 すると、赤の三角形の高さは\( a \sin \theta \)、青の三角形の底辺は\( b \cos \theta \)となる。
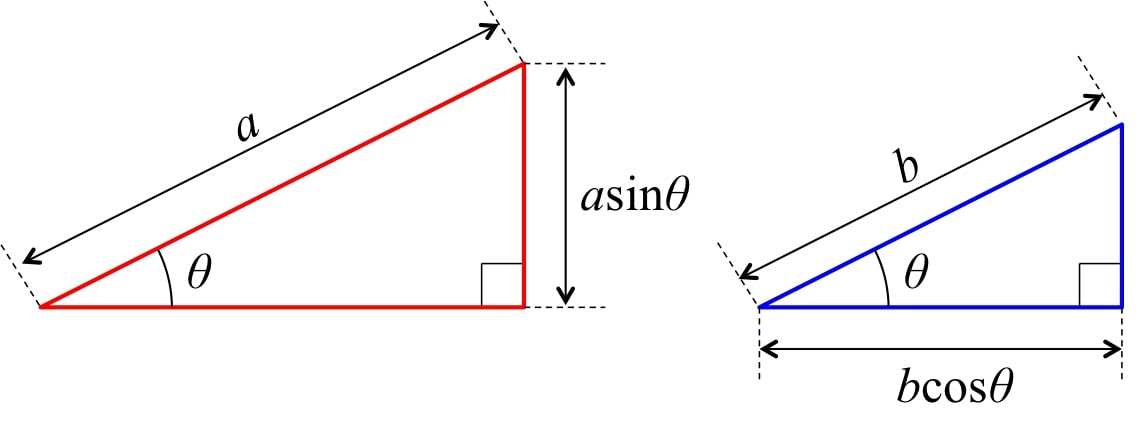
図1 相似形の直角三角形
赤の三角形の高さと、青の三角形の底辺の足し合わせが、式(1)の左辺である。 これらの辺を合わせて幾何学的に三角関係の合成を解いていく。 図1のように各辺を合わせる。 緑の直線は、\( a \sin \theta + b\cos \theta \)と同じ長さの直線である。 角度\( \alpha \)を図1のように取ると、緑の直線は以下の様に表すことができる。 \begin{eqnarray} \sin ( \theta + \alpha ) = \frac{a\sin \theta + b\cos \theta}{\sqrt{a^2 + b^2}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} となる。これを整理すると、式(1)の三角関数の合成の式を得ることができる。
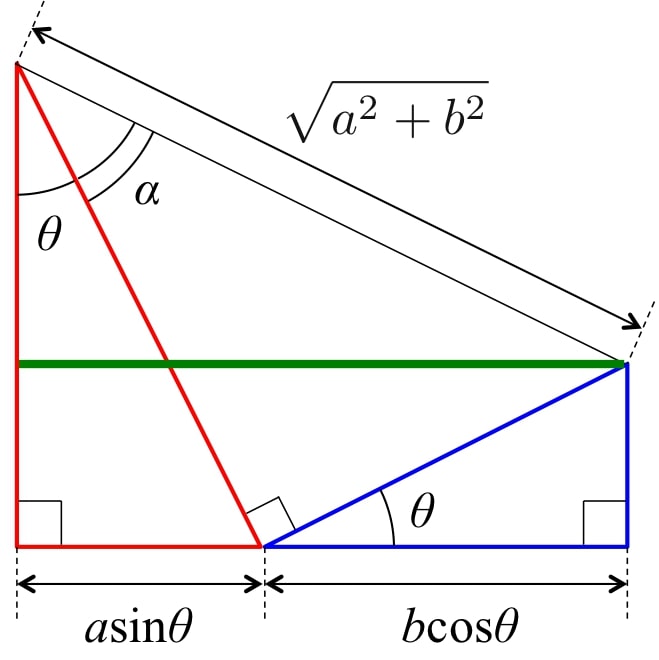
図1 相似形の直角三角形
ここで、図1から自明であるが、\( \alpha \)は \begin{eqnarray} \sin \alpha &=& \frac{b}{\sqrt{a^2 + b^2}} \\ \cos \alpha &=& \frac{a}{\sqrt{a^2 + b^2}} \\ \tan \alpha &=& \frac{b}{a} \end{eqnarray} と表される。