三角関数（加法定理）

三角関数の加法定理は以下のように表される。 \begin{eqnarray} \sin (\alpha \pm \beta) &=& \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ \cos (\alpha \pm \beta) &=& \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\ \tan (\alpha \pm \beta) &=& \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} \end{eqnarray} 三角関数の加法定理は覚えやすいので、記憶することをオススメするが、興味がある人のために加法定理の証明を以下に示しておく。

図1のような単位円と単位円上の点Pと点Qを考える。OQ、OPとx軸のなす角をそれぞれ\( \alpha \)、\( \beta \)とする。 点Pの座標は\( (\cos \beta,\ \sin \beta ) \)、点Qの座標は\( (\cos \alpha,\ \sin \alpha ) \)となる。 PQの長さは点Pと点Qの座標の関係から \begin{eqnarray} |PQ|^2 &=& (\cos\alpha - \cos \beta)^2 + (\sin\alpha - \sin \beta)^2 \\ &=& \cos^2\alpha - 2 \cos \alpha \cos \beta + \cos^2 \beta + \sin^2 \alpha -2 \sin \alpha \sin \beta + \sin^2 \beta \\ &=& 2 - 2 ( \cos \alpha \cos \beta + \sin \alpha \sin \beta ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} となる。

今度は余弦定理から \begin{eqnarray} |PQ|^2 = |OP|^2 + |PQ|^2 - 2|OP||OQ|\cos \angle QOP\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} の関係が得られる。点Pと点Qは単位円上の点なので、\( |OP| = |OQ| = 1 \)である。 さらに\( \angle QOP = \alpha - \beta \)である。これを式(2)に代入する。

すると、 \begin{eqnarray} |PQ|^2 &=& 1 + 1 - 2 \cos (\alpha - \beta) = 2 - 2 \cos (\alpha - \beta)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} の関係が得られる。式(1)と式(3)から \begin{eqnarray} 2 - 2 \cos (\alpha - \beta) &=& 2 - 2 ( \cos \alpha \cos \beta + \sin \alpha \sin \beta ) \\ \cos (\alpha - \beta) &=& \cos \alpha \cos \beta + \sin \alpha \sin \beta\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) \end{eqnarray} を得ることができる。

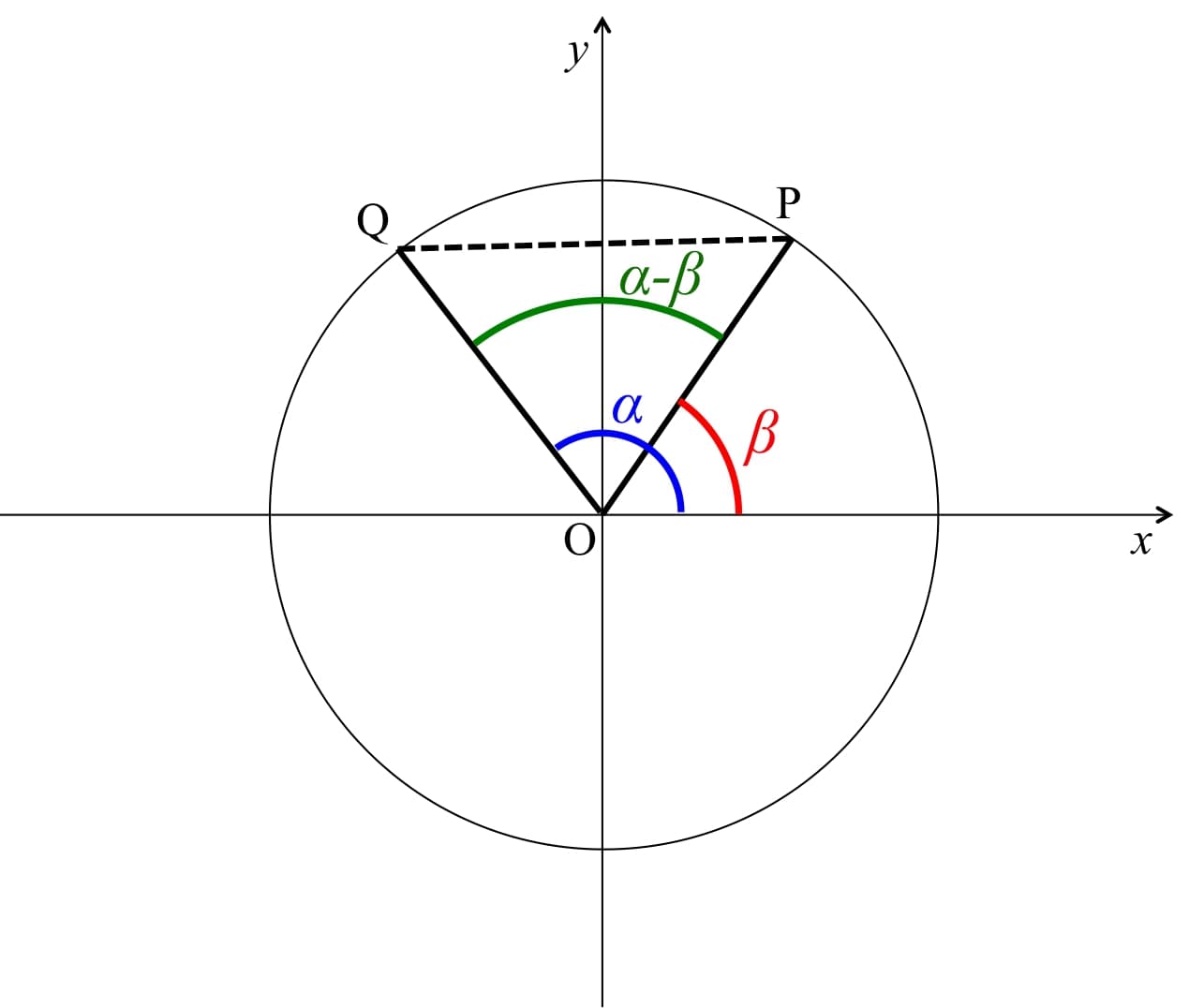
図1 単位円上の点Pと点Qと原点を結んだ直線とx軸がなす角αとβの関係

式(4)が得られれば他の定理もすぐに明らかにできる。 \begin{eqnarray} \cos(\alpha + \beta) &=& \cos(\alpha -(- \beta) ) = \cos \alpha \cos(- \beta) + \sin \alpha \sin(- \beta) \\ &=& \cos \alpha \cos \beta - \sin \alpha \sin \beta\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} 次は少し工夫して変換する。 \begin{eqnarray} \cos\left( \frac{\pi}{2} - (\alpha + \beta) \right) &=& \cos\left( ( \frac{\pi}{2} - \alpha ) + \beta)\right) \\ &=& \sin (\alpha + \beta) \\ &=& \cos (\frac{\pi}{2} - \alpha) \cos \beta + \sin (\frac{\pi}{2}-\alpha) \sin \beta \\ &=& \sin \alpha \cos \beta + \cos \alpha \sin \beta\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} また、 \begin{eqnarray} \sin\left( \alpha - -(-\beta) \right)&=& \sin \alpha \cos(-\beta) + \cos \alpha \sin(-\beta) \\ &=& \sin \alpha \cos \beta - \cos \alpha \sin \beta\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} を導くことができ、加法定理を得ることができる。