三角関数（基礎）

三角関数は図1に示す単位円常に太線で表された三角\( OPQ \)を用いて以下のように定義される。 \begin{eqnarray} \sin \theta &=& \frac{PQ}{OP} \\ \cos \theta &=& \frac{OQ}{OP} \\ \tan \theta &=& \frac{PQ}{OQ} = \frac{\sin \theta}{\cos \theta} \end{eqnarray} これらは中学、高校で基本的なことを習うので詳しくは説明しない。 サイン（ \( \sin \) ）、コサイン（\( \cos \)）、タンジェント(\( \tan \))はそれぞれ、正弦、余弦、正接と呼ばれる。

大学の物理の授業では、これらの逆数を以下のように表すと便利なためよく用いられる。 \begin{eqnarray} \cot \theta &=& \frac{1}{\tan \theta} \\ \sec \theta &=& \frac{1}{\cos \theta} \\ \csc \theta &=& \frac{1}{\sin \theta} \end{eqnarray} \( \cot \)はコタンジェント（余接）、\( \sec \)はセカント（正割）、\( \csc \)はコセカント（余割）と呼ぶ。 図2に正弦、余弦、正接、余接、正割、余割それぞれの関係を示す。

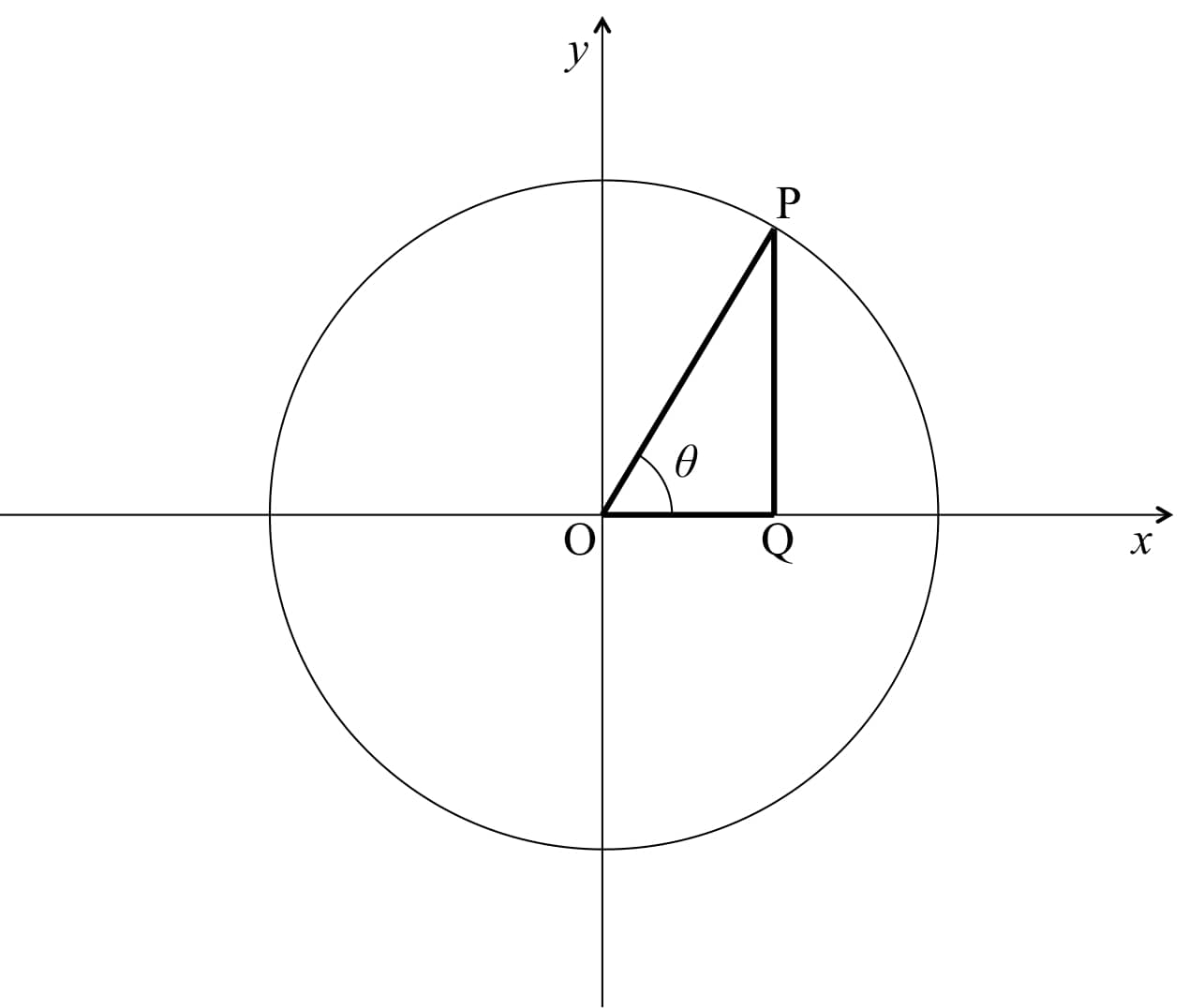
図1 単位円上の点Pと点Pからx軸に垂直に下ろした点Qと原点Oで表される直角三角形

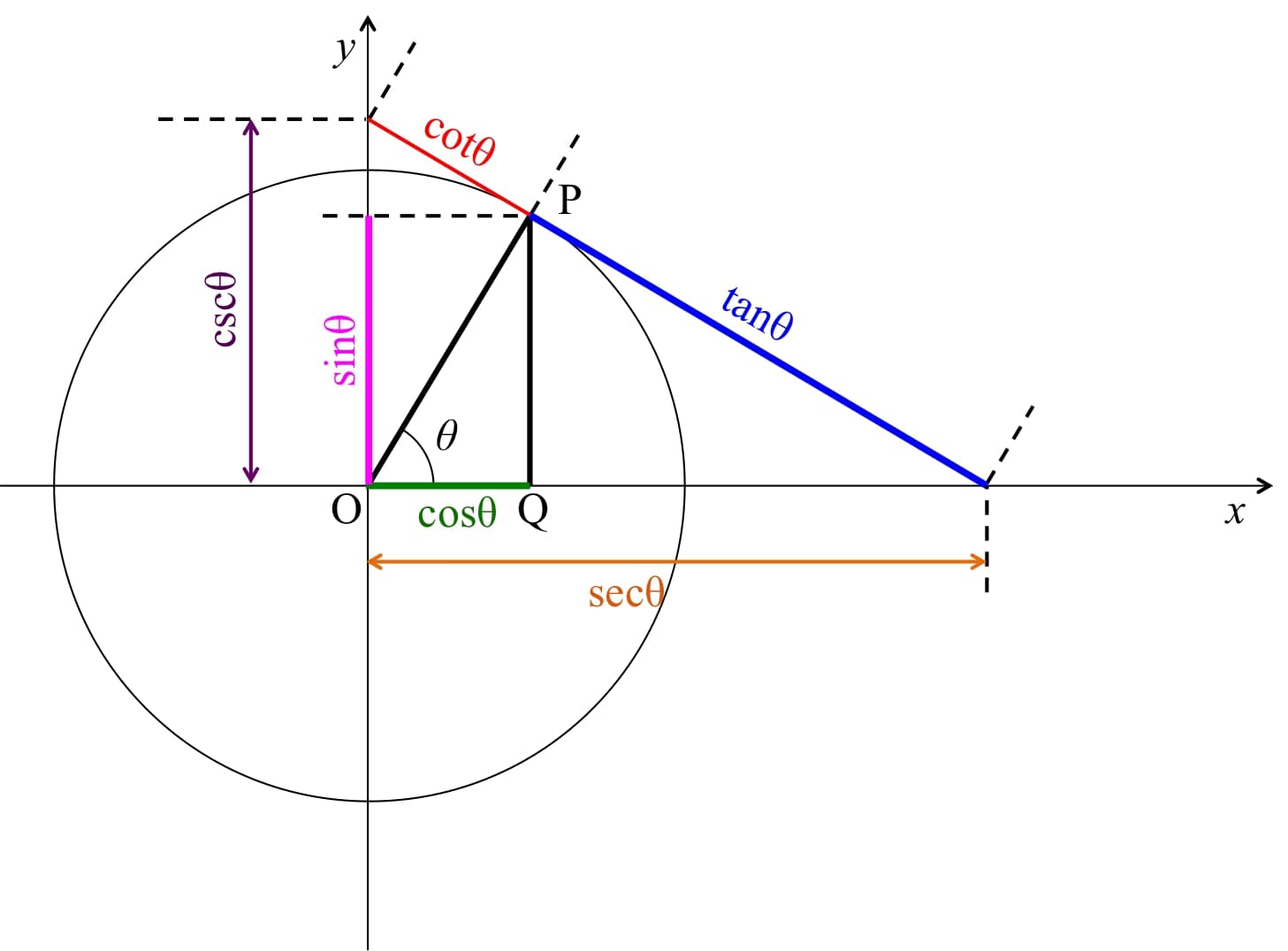
図2 正弦、余弦、正接、余接、正割、余割の関係