オイラーの公式
オイラーの公式とは虚数\( i \)を肩に持つ指数関数と三角関数との関係性を示すものである。 一般的な関係として、以下の関係がよく用いられる。
\begin{eqnarray} e^{i \theta} &=& \cos \theta + i \sin \theta \ \ \ \ \ \ \ \ \ \ \ \ \ (1)\\ e^{-i \theta} &=& \cos \theta - i \sin \theta \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray}このオイラーの公式とは、その実部と虚部は\( \theta \)にどのような値を代入しても、周期的に変化するということを示したものである。 文字で説明しても、わかりにくいので、証明を後回しにして式(1)をマクローリン展開することで少しその意味を紐解いてみる。
指数関数\( e^{i\theta} \)をマクローリン展開すると以下のようになる。
\begin{equation}
e^{i \theta} = \sum_{n=0}^{\infty} \frac{(i \theta)^n}{n!} = 1 + i\theta - \frac{\theta^2}{2} - i \frac{\theta^3}{6} + \frac{\theta^4}{24} + i \frac{\theta^5}{120} - \frac{\theta^6}{720} - \cdots \ \ \ \ \ \ \ \ \ \ \ \ \ (3)
\end{equation}
ここで、虚数の項(虚部)、それ以外(実部)に分ける。
\begin{equation}
e^{i \theta} = \sum_{n=0}^{\infty} \frac{(i \theta)^n}{n!} = \left( 1 - \frac{\theta^2}{2} + \frac{\theta^4}{24} - \frac{\theta^6}{720} + \cdots \right) + i\left( \theta - \frac{\theta^3}{6} + \frac{\theta^5}{120} - \cdots \right) \ \ \ \ \ \ \ \ \ \ \ \ \ (4)
\end{equation}
この右辺、第1項目が実部で2項目が虚部である。試しに、\( \theta \)に1を代入してみると、式(4)の実部は0.540、虚部は0.841となる。
では、\( \theta \)に3を代入してみると、実部は-0.990、虚部は0.141となる。
実部は符号が変わり、絶対値が大きくなった。虚部は小さくなった。
他の値を代入してみればわかるが、\( \theta \)にどんなに大きな値を代入しても、1を超えることはなく、ずっと-1と1の間を循環するのみなのである。
では\( \theta \)に様々な値を代入した時に実部と虚部はどのように変化するのであろうか?
それを図1に示す。
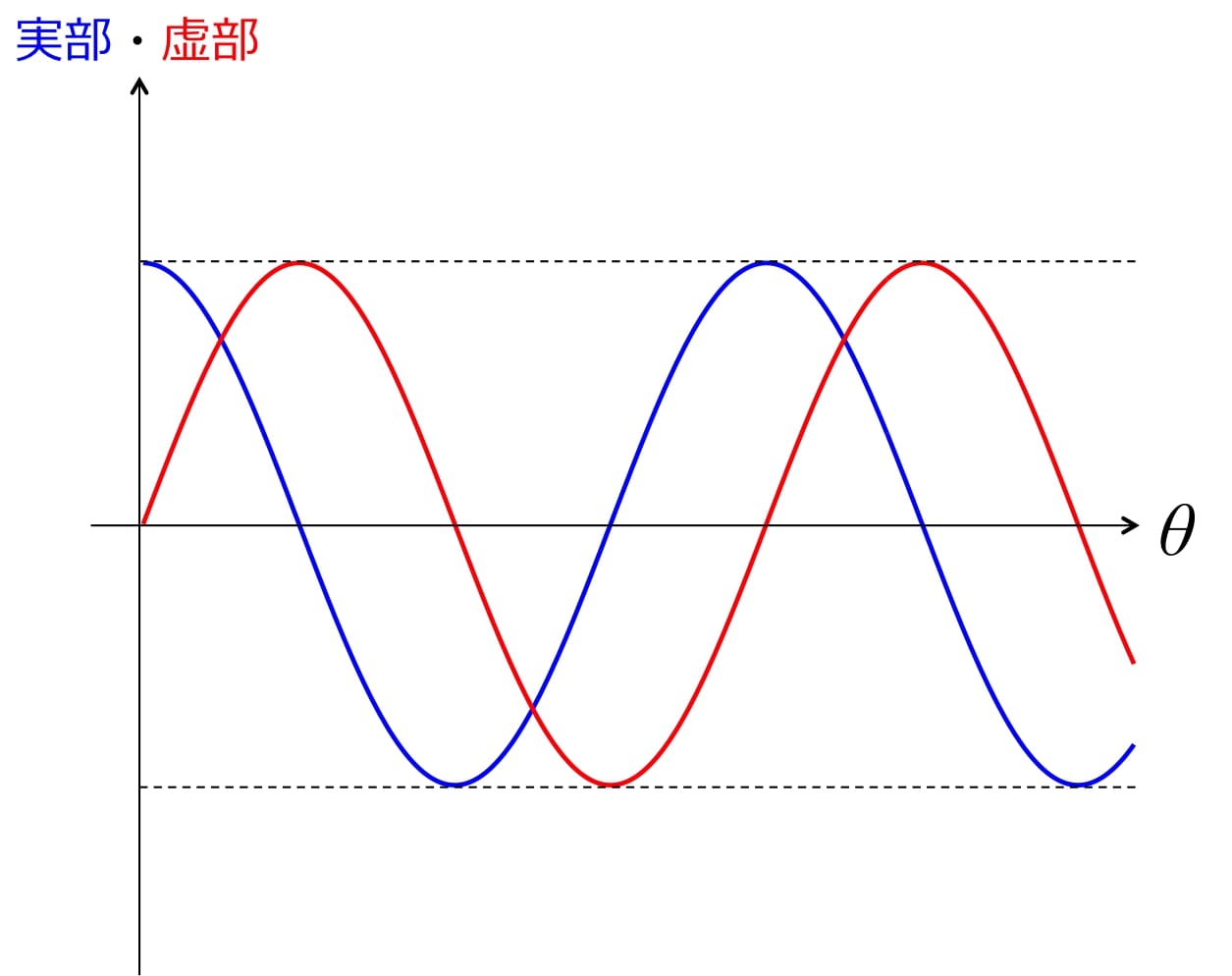
図1 実部、虚部とθの関係
ここまで示せばだんだんわかってくるのだが、実部は\( \cos \theta \)、虚部は\( \sin \theta \)で変化していることがわかる。 よって、実部と虚部の関係を示す。ここで、よくされる表記法として、実部をRe、虚部をImが用いられるので、この図でもその表記に従って示す。 (ReはReal、ImはImaginaryの略)
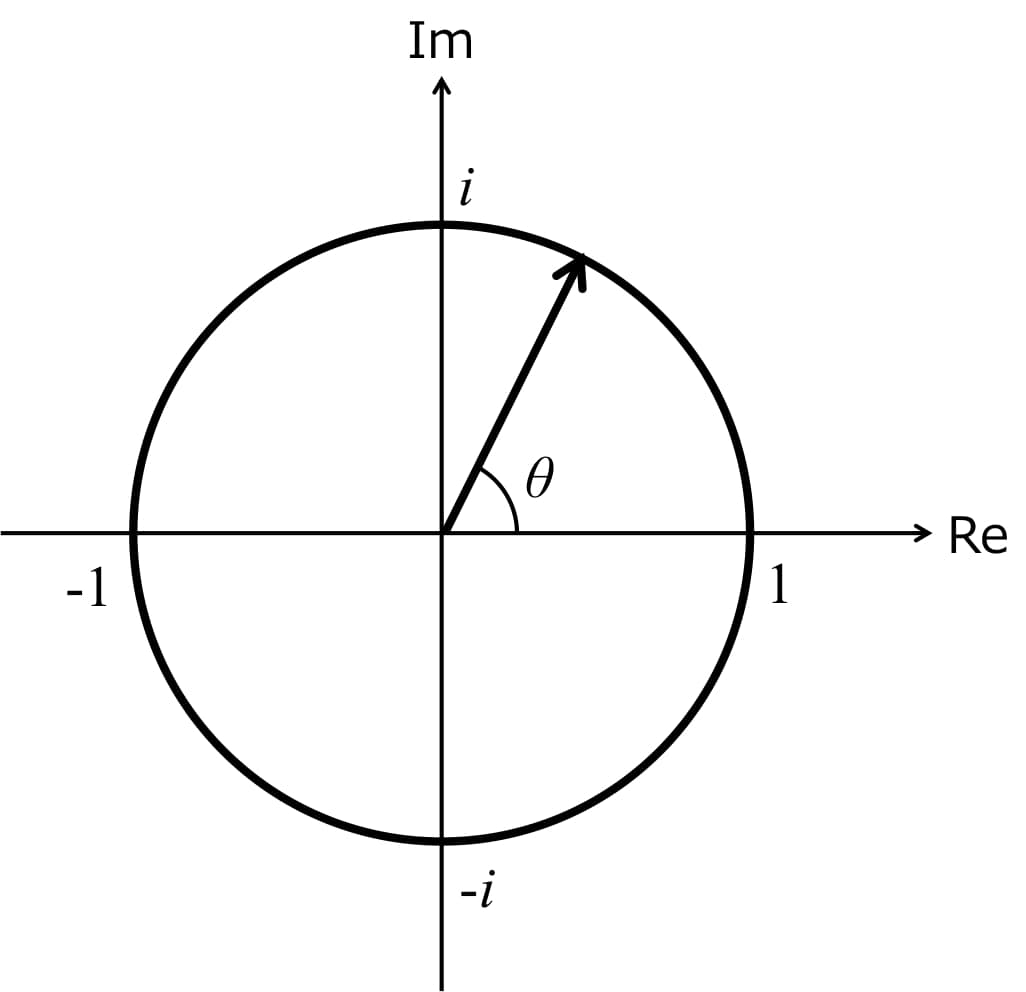
図2 実部と虚部の関係
図2から\( e^{i\theta} \)の虚部と実部はθの値によって、周期的に変動するのである。 一般的に指数関数の指数(ここで言うθ)を大きくするとそれに伴い値も大きくなるのだが、指数に虚数がある関係でその性質は大きく変えられるのである。 虚数を指数に含む指数関数が三角関数で表すことができるこの公式を
オイラーの公式
と呼ぶ。 オイラーの公式は人類が発見した方程式の中でも最も美しい方程式と言っても過言ではない。 次にオイラーの公式の証明を行う。オイラーの公式の証明
数学者であり、天文学者であるレオンハルト・オイラーは\( e^{i \theta} \)と三角関数の級数展開(一定の規則で並んだ数列のこと:マクローリン展開)を比較することで、オイラーの公式を見つけ出した。 オイラーの方程式はその美しさに反して導出方法はマクローリン展開(テイラー展開)さえ知っていれば驚くほど簡単である。 まず、上にも示したが、\( e^{i\theta} \)のマクローリン展開を示す。 \begin{equation} e^{i \theta} = \sum_{n=0}^{\infty} \frac{(i \theta)^n}{n!} = \left( 1 - \frac{\theta^2}{2} + \frac{\theta^4}{24} - \frac{\theta^6}{720} + \cdots \right) + i\left( \theta - \frac{\theta^3}{6} + \frac{\theta^5}{120} - \cdots \right) \ \ \ \ \ \ \ \ \ \ \ \ \ (1.13.5) \end{equation} 次に、正弦・\( \sin \theta \)と余弦・\( \cos \theta \)のマクローリン展開を示す。 \begin{eqnarray} \sin x &=& \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{(2n+1)} = \theta - \frac{\theta^3}{6} + \frac{\theta^5}{120} - \cdots \\ \cos x &=& \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} x^{2n} = 1 - \frac{\theta^2}{2} + \frac{\theta^4}{24} - \frac{\theta^6}{720} + \cdots \end{eqnarray} 三角関数のマクローリン展開と\( e^{i \theta} \)のマクローリン展開とを比較することで容易に、 \begin{equation} e^{i \theta} = \cos \theta + i \sin \theta \ \ \ \ \ \ \ \ \ \ \ \ \ (1.13.1) \end{equation} を導くことができる。色々な教科書やウェブサイトで様々な導出方法が紹介されているが、この方法がオイラーが導出した方法と極めて近いのである。