単振り子
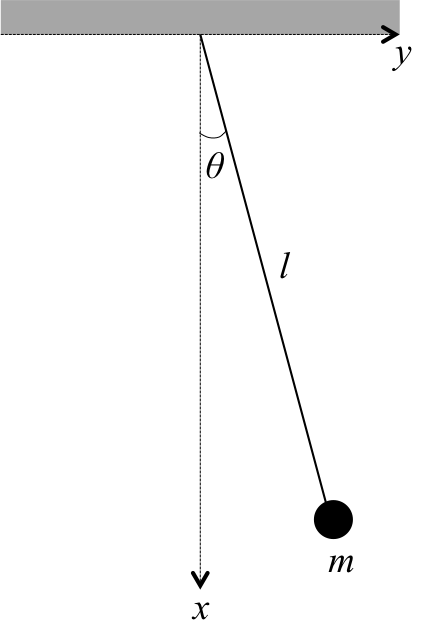
図2-5 単振り子
単振り子の場合は1次元ではなく2次元の運動になる。
この場合、運動エネルギー\( T \)は
\begin{equation}
T = \frac{1}{2} m \dot{x}^2 + \frac{1}{2} m \dot{y}^2
\end{equation}
と書ける。ここで極座標系に書き換えると
\begin{eqnarray}
\dot{x} &=& \dot{l}\cos \theta - l \dot{\theta} \sin \theta \\
\dot{y} &=& \dot{l}\sin \theta + l \dot{\theta} \cos \theta
\end{eqnarray}
であり、糸の長さ\( l \)は時間変化しないので、\( \dot{l}=0 \)である。
よって、運動方程式は極座標系で
\begin{equation}
T = \frac{1}{2} m l^2 \dot{\theta}^2
\end{equation}
と書き直される。糸と天井がつながれている点を原点として、下向きを正とすると、位置エネルギーは
\( l\cos\theta \)であるので、ポテンシャル・エネルギー\(U\)は
\begin{equation}
U = -mgl\cos\theta
\end{equation}
と表される。この系のラグラジアン\( {\cal L} \)は
\begin{equation}
{\cal L} = L - U = \frac{1}{2} m l^2 \dot{\theta}^2 + mgl\cos\theta
\end{equation}
と表される。ラグラジアンをラグランジュ方程式
\begin{equation}
\frac{d}{dt} \left( \frac{\partial {\cal L}}{\partial \dot{\theta}} \right) = \frac{\partial {\cal L}}{\partial \theta}
\end{equation}
に代入することで、運動方程式は
\begin{equation}
l\ddot{\theta} = - g \sin{\theta}
\end{equation}
となる。
広告

