滑車を通してばねとつながれた2つの質点
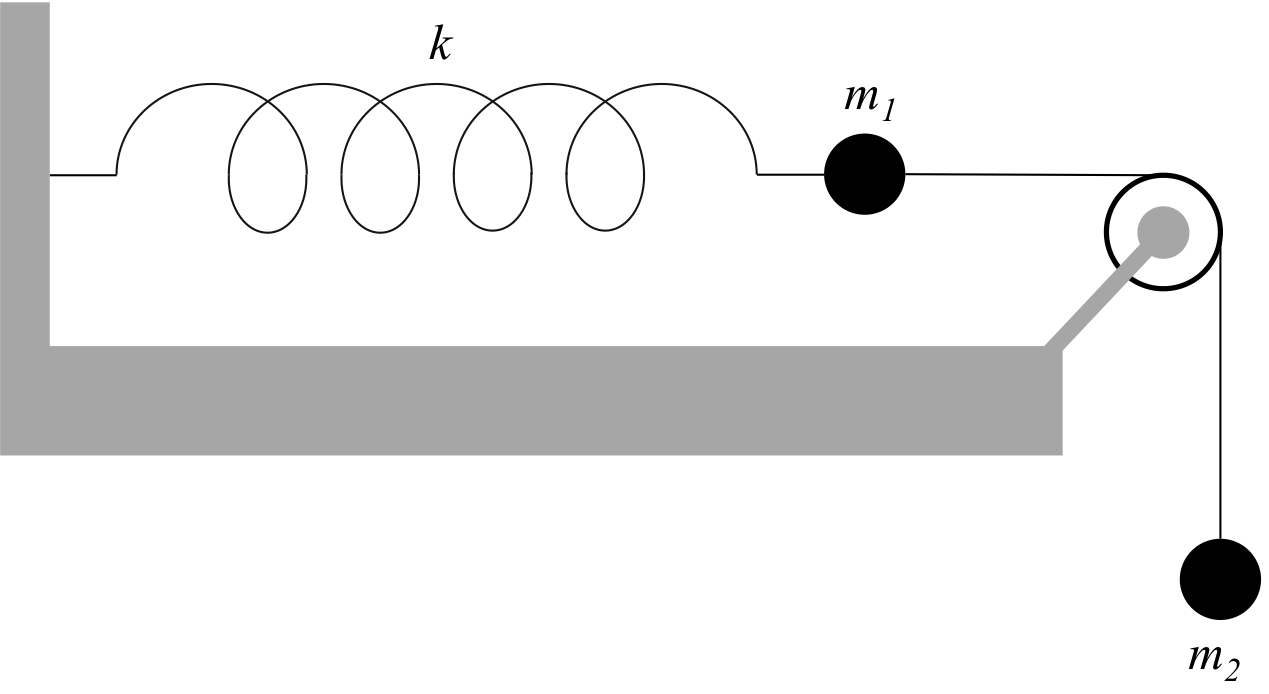
図2-3 滑車を通してばねとつながれた2つの質点
重力加速度は鉛直下向きに\(g\)、摩擦はなく、ばねはフックの法則に従い、
自然長からの伸びを\(x\)とする。
質点が2つの以上の場合、ラグランジュ方程式を用いると非常に便利である。
2つの質点は糸で結ばれているので変異\( x \)は同じであることに注意すると
この系の運動エネルギーは
\begin{equation}
T = \frac{1}{2} \left( m_1 + m_2 \right) \dot{x}^2
\end{equation}
である。この系に働く力\(F\)は
\begin{equation}
F = -kx + m_2 g
\end{equation}
であるので、力とポテンシャルエネルギーの関係を使って、ポテンシャルエネルギー\(U\)は
\begin{equation}
U = \frac{1}{2} kx^2 - m_2 gx
\end{equation}
となるのでラグラジアンは
\begin{equation}
{\cal L} = T - U = \frac{1}{2} \left( m_1 + m_2 \right) \dot{x}^2 - \frac{1}{2} kx^2 + m_2 gx
\end{equation}
と導かれる。以上により、この系のラグラジアンを求めることができた。
運動方程式はラグランジュ方程式に代入することで求めることができる。
\begin{equation}
\frac{d}{dt} \left( \frac{\partial {\cal L}}{\partial \dot{x}} \right) = \frac{\partial {\cal L}}{\partial x}
\end{equation}
より、
\begin{eqnarray}
\frac{d}{dt} \left( m_1 + m_2 \right) \dot{x} &=& -kx + m_2 g \\
\left( m_1 + m_2 \right) \ddot{x}&=& -kx + m_2 g
\end{eqnarray}
と求められる。
広告
