減衰振動：エネルギーの減少

　力学の問題で出ている問題の多くは摩擦や空気抵抗がない場合がほとんどである。 こういった場合では、振動を開始させるとその質点は永遠に振動をしている。 しかし、現実では振り子はやがて空気抵抗によって振動を止められてしまうし、ばねによる振動では接地面での摩擦によってやがて振動は止まってしまう。このように物体は抵抗によってその運動を抑制されてしまう。 特に抵抗によって振幅が小さくなっていく調和振動のことを減衰振動と呼ぶ。 このページでは減衰振動によってエネルギーがどのように失われていくのかを見ていこうと思う。 この時、エネルギーとは運動エネルギーとポテンシャルエネルギーの和である力学的エネルギーのことを示している。

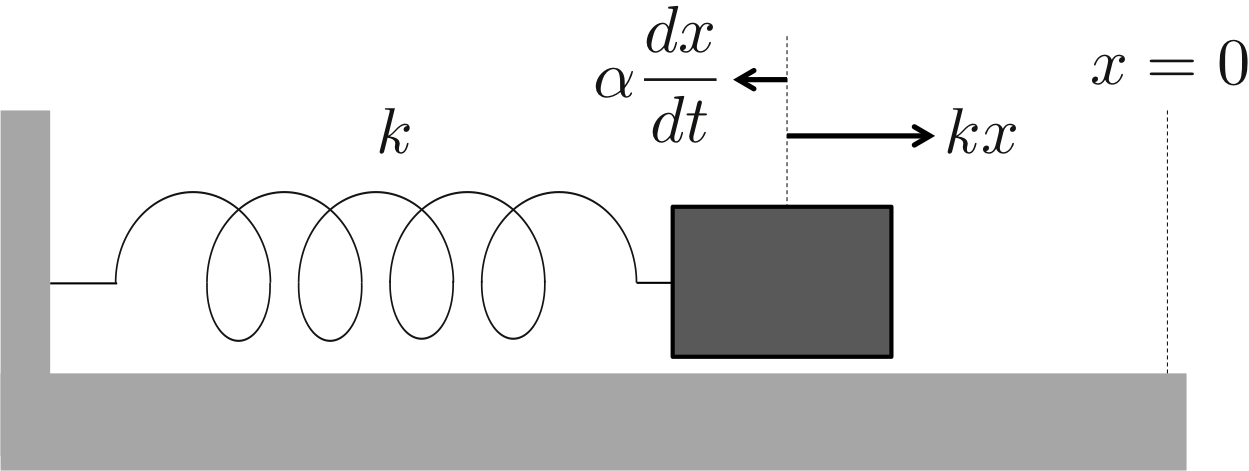
図1.　摩擦のある面でのばねによる調和振動

　図1のように摩擦ある面にばねに繋がれた物体を置き、運動させる。 摩擦力は定数を\( \alpha\)として、\( \alpha \frac{dx}{dt} \)と表され、フックの法則にしたがうばねによる力\( kx \)と共に質点に働く。よって運動方程式を以下のように立てることができる。 \begin{eqnarray} m \frac{d^2 x}{dt^2} = -kx - \alpha \frac{dx}{dt}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} ここで運動方程式(1)の右辺について少し説明する。 復元力を運動方程式中で\( -kx \)と示すことができることは何度も出てきているので特に説明しないが、摩擦力は復元力とは少し違うので注意が必要である。
　復元力は\( x=0 \)の釣り合いの位置でその向きが変わるが、摩擦力は物体（質点）の運動の向きと反対にかかる。 つまり、\( x \)の時間変化\( \frac{dx}{dt} \)を考えればよくて、右向きの正に進んでいる（\(x\)が増加）ときは左向きに摩擦力がかかり、左向きに進んでいる（\(x\)が減少）ときは右向きに摩擦力がかかる。 よって、\( x\)の増減と摩擦力の正負が反対になるので、式(1)の右辺のようにマイナスが付いて\( - \alpha \frac{dx}{dt} \)となるのである。
　では式(1)から減衰振動によってエネルギーが減少していくことを示そう。 式(1)の両辺に\( \frac{dx}{dt} \)をかけると、 \begin{eqnarray} m \frac{dx}{dt}\frac{d^2 x}{dt^2} = - \alpha \left( \frac{dx}{dt} \right)^2 - kx\frac{dx}{dt}\ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} を得る。ここで、 \begin{align} \frac{dx}{dt}\frac{d^2 x}{dt^2} &= \frac{1}{2} \frac{d}{dt} \left( \frac{dx}{dt} \right)^2\ \ \ \ \ \ \ &(3) \\ x \frac{dx}{dt} &= \frac{1}{2} \frac{d}{dt} x^2 &(4) \end{align} である関係を使うと式(2)は以下のように書き換えることができる。 \begin{eqnarray} \frac{d}{dt} \left\{ \frac{1}{2}m\left( \frac{dx}{dt}\right)^2 + \frac{1}{2}kx^2 \right\} = - \alpha \left( \frac{dx}{dt} \right)^2 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) \end{eqnarray} ここで、右辺の括弧内は力学的エネルギー\( E \)を示している。 右辺は\( \alpha \geq 0 \)であるので常に負か0である。 右辺が0になるのは\( \alpha \)が0でないならば、運動の方向が変わる転回点においてのみである。 よって、式(5)から力学的エネルギーは摩擦によってエネルギーが減少することがわかる。
　次にどのようにエネルギーが減少するのか見ていこうと思う。 式(5)の微分方程式を解くためには右辺も力学的エネルギー\( E \)で表さないといけいない。 まず、式(5)を振動の1周期にわたる平均を取る。 ここで、摩擦力\( \alpha \)は十分に弱いと仮定して、振動の1周期で失われるエネルギーは十分小さいを仮定する。 すると、ある時間、ある場所のにおける力学的エネルギーを示す、式(5)の右辺の力学的エネルギーの時間変化はすべての時間で一定であると仮定できる。 つまり、 \begin{eqnarray} \frac{d}{dt} E = - \alpha \overline{ \left( \frac{dx}{dt} \right)^2 } \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6) \end{eqnarray} を得ることができる。 また、1周期にわたる運動エネルギーの平均は力学的エネルギーの半分になる。 なぜ、1周期にわたる運動エネルギーの平均が力学的エネルギーの半分になるかは調和振動子の力学的エネルギーのページを参照して欲しい。 よって、以下のような関係式が導ける。 \begin{eqnarray} \overline{T} = \frac{1}{2} m \overline{\left( \frac{dx}{dt} \right)^2} = \frac{1}{2} E \ \ \ \ \ \ \ \ \ \ \ (7) \end{eqnarray} 式(7)を式(6)に代入することで、 \begin{eqnarray} \frac{d}{dt} E = - \frac{ \alpha}{m} E \ \ \ \ \ \ \ \ \ \ \ \ (8) \end{eqnarray} を得る。ここで、\( t=0 \)で\( E= E_0 \)という初期条件を与えることで式(7)の微分方程式を解くことができる。 \begin{eqnarray} E = E_0 \exp\left( - \frac{\alpha}{m} t \right)\ \ \ \ \ \ \ \ \ \ \ (9) \end{eqnarray} よって、摩擦による減衰振動では力学的エネルギーが指数関数的に減少するのである。

広告