調和振動が持つ解
バネや振り子のように位置に依存した力を復元力とする調和振動(単振動)は一般的に、以下の形の運動方程式になる。 \begin{eqnarray} \ddot{x} + \omega_0^2 x = 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} ここで、\( \omega_0\)は角振動数で、振り子の場合は振り子の長さを\( l\)とすると\( \omega_0^2 = \sqrt{g/l} \)となる。 この式をよく見ると、もし\(x\)が負になる場合は、\( \ddot{x} \)は正でなくてはならない。 逆にもし、\( x\)が正の場合は、\( \ddot{x} \)は負でなくてはならない。 つまり、釣り合いの位置を原点とすると、常に変位と反対方向に加速度が生まれるのである。 このことから、式(1)で示された微分方程式は振動する解になることが想定される。 振動解は三角関数を使って、\( \sin \omega t \)や\( \cos \omega t\)のように表される。 では、(1)の解を、\( x=A\cos(\omega t + \alpha_0) \)と置いてみる。 この時、\(A\)は振幅、\( \alpha_0 \)は初期位相である。 すると、\(x\)の2階微分は\( \ddot{x} = - A\omega^2 \cos(\omega t + \alpha_0) \)となるので、\( \omega =\omega_0 \)の時に式(1)の解となることがわかる。つまり、調和振動子の運動方程式の解は、 \begin{eqnarray} x = A \cos ( \omega_0 t + \alpha_0 ) \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} と書けることがわかる。 ちなみに、この調和振動の1周期は\( T = 2\pi / \omega_0 \)である。 \( \omega_0 \)は上でも述べたように角振動数である。 角振動数は調和振動のページでも説明されたように、バネによる振動の場合はバネ係数と質点の質量で表され、振り子の場合は糸の長さと重力加速度で表される。 このように角振動数は振幅や速度といった運動の状態によって変わらない量であるので、固有振動数とも呼ばれる。 では、この式(2)で示される解が調和振動の解となるわけだが、この式の初期位相\( \alpha_0 \)は何を意味するのか、\( \sin \)と置くことと何か違いはあるのだろうか?と言う疑問が残る。(物理数学でもう既に2階微分方程式の解き方を知っている人はそうではないかもしれないが) ではこの解について少し検証してみる。
初期位相\( \alpha_0 \)を解に含める理由は、「初期条件に対応するため」である。 図1の\( \cos ( \omega_0 t + \alpha_0 ) \)の\( \alpha_0 \)を変化させて計算したものをプロットする。 ここで、分かりやすいように振幅\( A \)は1とした。
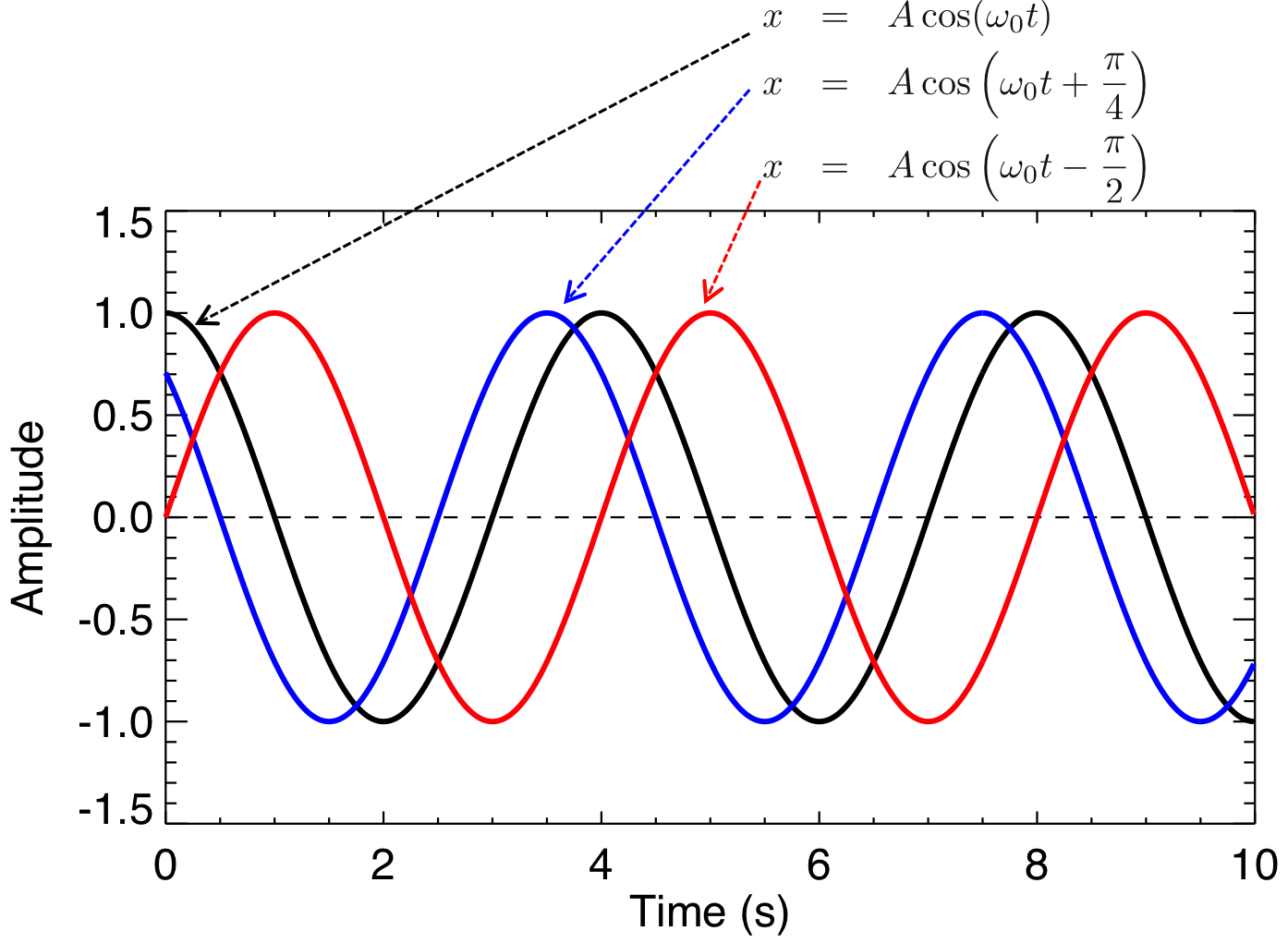
図1. \( A \cos ( \omega_0 t + \alpha_0 ) \)
式(2)を三角関数の加法定理によって展開すると以下のようになる。 \begin{eqnarray} x = A\cos \alpha_0 \cos \omega_0 t - A \sin \alpha_0\sin \omega_0 t\ \ \ \ \ \ \ (4) \end{eqnarray} この時、\( a = A\cos \alpha_0 \)、\( b= - A \sin \alpha_0 \)とおく。 この\( a\)と\( b\)は時間によって変化しないので、定数として取り扱える。 よって式(4)は、 \begin{eqnarray} x = a \cos \omega_0 t + b \sin \omega_0 t\ \ \ \ \ \ \ (5) \end{eqnarray} となることがわかる。調和振動を表す解として、式(2)を用いても式(5)を用いても良い。 参考書などでは式(5)を用いて解いているものの方が多いかもしれない。
式(2)では\( A \)と\( \alpha_0 \)を式(5)では\( a \)と\(b\)を未知数として含んでいる。 これは微分方程式を解く際に現れる積分定数であり、これらの未知数は初期条件という\( t=0 \)での条件がわかればその値を知ることができるのである。
初期条件として、\( t=0 \)で\(x=x_0\)、\( v = \dot{x} = 0 \)であった場合、式(2)とそれを1階微分した式に\( t=0 \)を入れてみると、 \begin{eqnarray} x &=& A \cos\ \alpha_0 = x_0 \\ v= \dot{x} &=& - A \omega_0\sin\ \alpha_0 = 0 \end{eqnarray} の連立方程式を得る。\( A \)と\( \omega_0\)は0ではないので、上の連立方程式を満足する解は、\( \alpha_0 = 0 \)、\( A = x_0 \)となることがわかる。よって、式(2)は \begin{eqnarray} x = x_0 \cos \omega_0 t \end{eqnarray} となり、すべての未知数が分かったことになる。
では、最後に初期条件として\( t=0\)で\( x=x_0\)、\( v = v_0 \)であった場合に式(5)の未知数がどう求められていくか示す。 初期条件を式(5)に代入すると以下の関係式が得られる。 \begin{eqnarray} a &=& x_0 \\ b\omega_0 &=& v_0 \end{eqnarray} 以上より、式(5)は \begin{eqnarray} x = x_0 \cos\omega_0 t + \frac{v_0}{\omega_0} \sin\omega_0 t \end{eqnarray} となり、未知数が消えたことがわかる。これは、式(2)で解いても同じ式が得られるが、解き方が少し面倒くさいので式(5)を使った方が簡単である。 このように調和振動の問題を解く際はまず運動方程式を立て、その階として式(2)または式(5)を考える。 最後に初期条件から未知数を明らかにすれば良いのである。
広告