English / Japanese

Brewster's angle

The intensity of a reflected p-polarized light is gradually decreased by increasing the incident angle. The reflection intensity of the p-polarized light becomes zero. After that, it increases with the increasing the incident angle. The incident angle for which the p-polarized light becomes zero is called the Brewster's angle. In this page, I intend to describe how to derive the Brewster's angle.

We consider the case in which the light is incident from a medium A to B as shown in Figure 1. The light partially is reflected and incident at the boundary. The intensity of this light depends on Fresnel’s law.

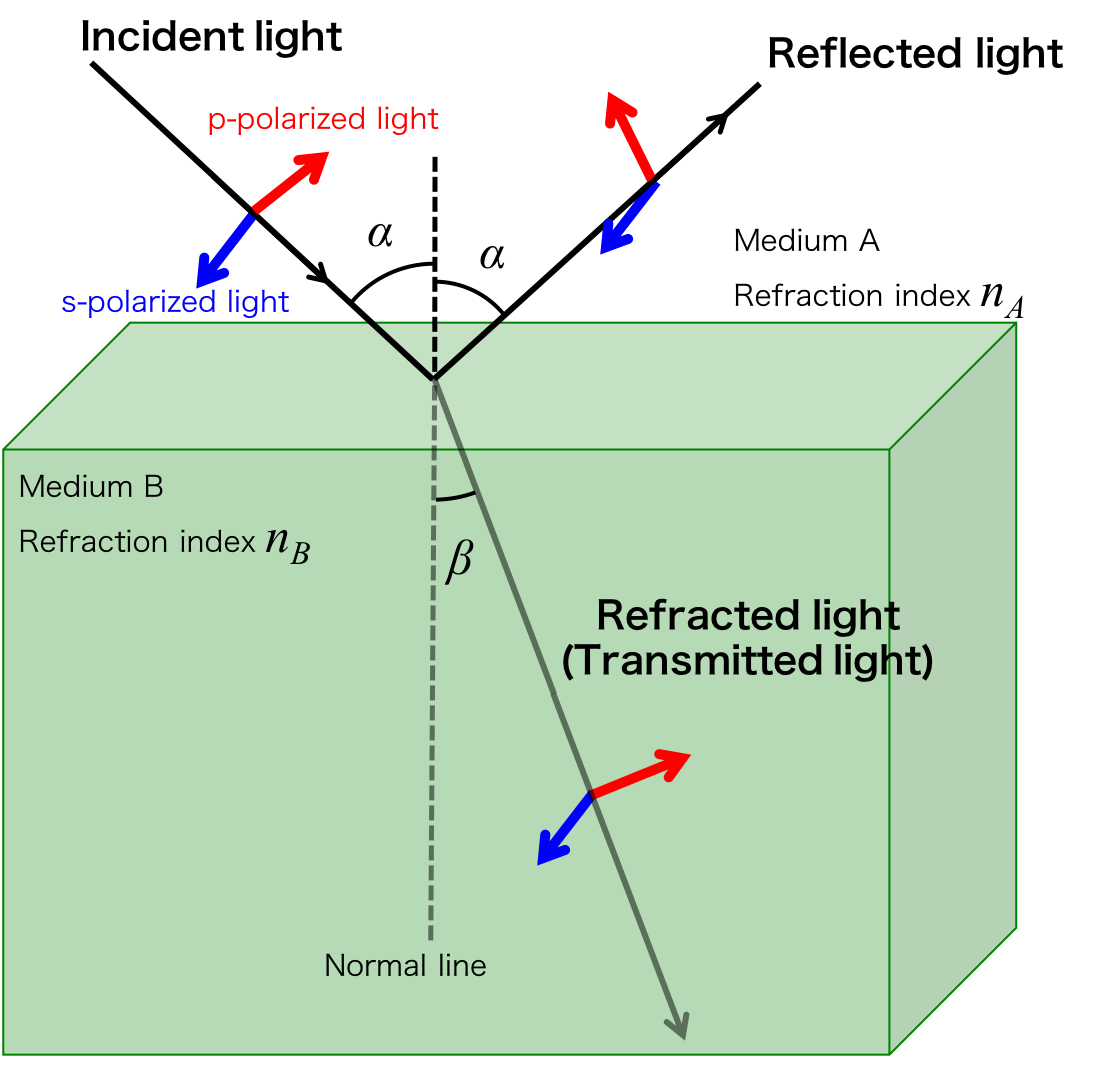
Figure 1. The reflected, refracted, and incident light and angles.

The Fresnel’s law is expressed as follows: \begin{eqnarray} t_p &=& \frac{2 n_A \cos \alpha}{n_B \cos \alpha + n_A \cos \beta} = \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)\cos(\alpha - \beta)} \\ r_p &=& \frac{n_B \cos \alpha - n_A \cos \beta}{n_B \cos \alpha + n_A \cos \beta} = \frac{\tan(\alpha - \beta)}{\tan(\alpha + \beta)} \\ t_s &=& \frac{2n_A \cos \alpha}{n_A \cos \alpha + n_B \cos \beta} = \frac{2 \sin \beta \cos \alpha}{\sin(\alpha + \beta)} \\ r_s &=& \frac{n_A \cos \alpha - n_B \cos \beta}{n_A \cos \alpha + n_B \cos \beta} = - \frac{\sin(\alpha - \beta)}{\sin(\alpha + \beta)} \end{eqnarray} where \( t_p \) and \( r_p \) are the incident and reflected amplitude rates for the p-polarized light and \( t_s \) and \( r_s \) the incident and reflected amplitude rates for the s-polarized light. The intensity of the incident and reflected light is expressed as follows: \begin{eqnarray} T_{p,\ s} &=& \frac{n_B \cos \theta_B}{n_A \cos \theta_A} | t_{p,\ s} | ^2 \\ R_{p,\ s} &=& | r_{p,\ s} | ^2 \end{eqnarray} where \( T_{p,\ s} \) and \( R_{p,\ s} \) are transmitted and reflected light intensity. The variation of the intensity of the reflected light with a changing incident angle \(\alpha\) is showed in Figure 2.

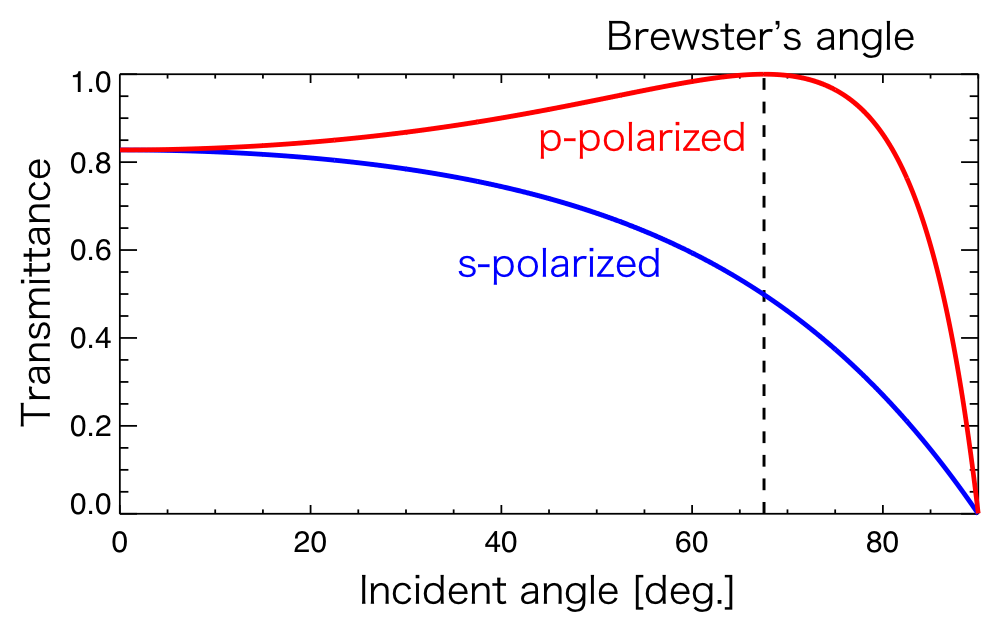
Figure 2. The intensity of them reflected the p- and s-polarized light entering from vacuum to diamond.

The intensity of the reflection light with s-polarization increases with an increasing incident angle \(\alpha\). On the other hand, the intensity of the reflection light with p-polarization decreases with an increasing incident angle and reaches zero, after increasing. The angle for which the reflection intensity of p-polarized light is zero is called the Brewster's angle. If the incident angle is the Brewster's angle \( \alpha_B\), the reflected angle is perpendicular to the refracted angle. Thus, \( \beta = 90^{\circ} - \alpha_B \) and we obtain the following relation by substituting \(r_p=0\) to Fresnel’s equation: \begin{eqnarray} \frac{\sin \alpha_B}{\cos \alpha_B} = \tan \alpha_B = \frac{n_B}{n_A} \end{eqnarray} Thus, \begin{eqnarray} \alpha_B = \arctan{\frac{n_B}{n_A}} \end{eqnarray} The intensity of the transmitted p- and s-polarized light entering from vacuum to diamond can be observed in Figure 3.

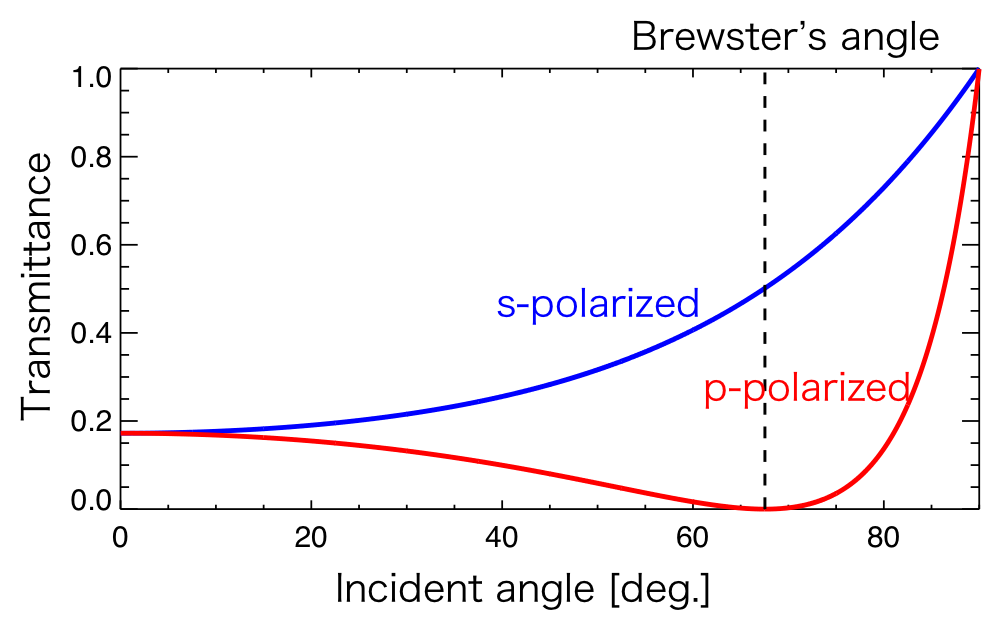
Figure 3 The intensity of the transmitted light.

According to Figure 2, the p-polarized light completely transmits to the medium with the Brewster's angle, as the relationship intensity of the transmitted and reflected light is: \begin{eqnarray} T_{p,\ s} + R_{p,\ s} = 1 \end{eqnarray}

Sponsored link