English / Japanese

Total Reflection

　Here we consider that light transmits from medium A to B as shown in Figure 1. In this consideration, the refractive index of medium A is larger than the refractive index of medium B (\( n_A > n_B\)). It is a same case that light transmits from water to air.

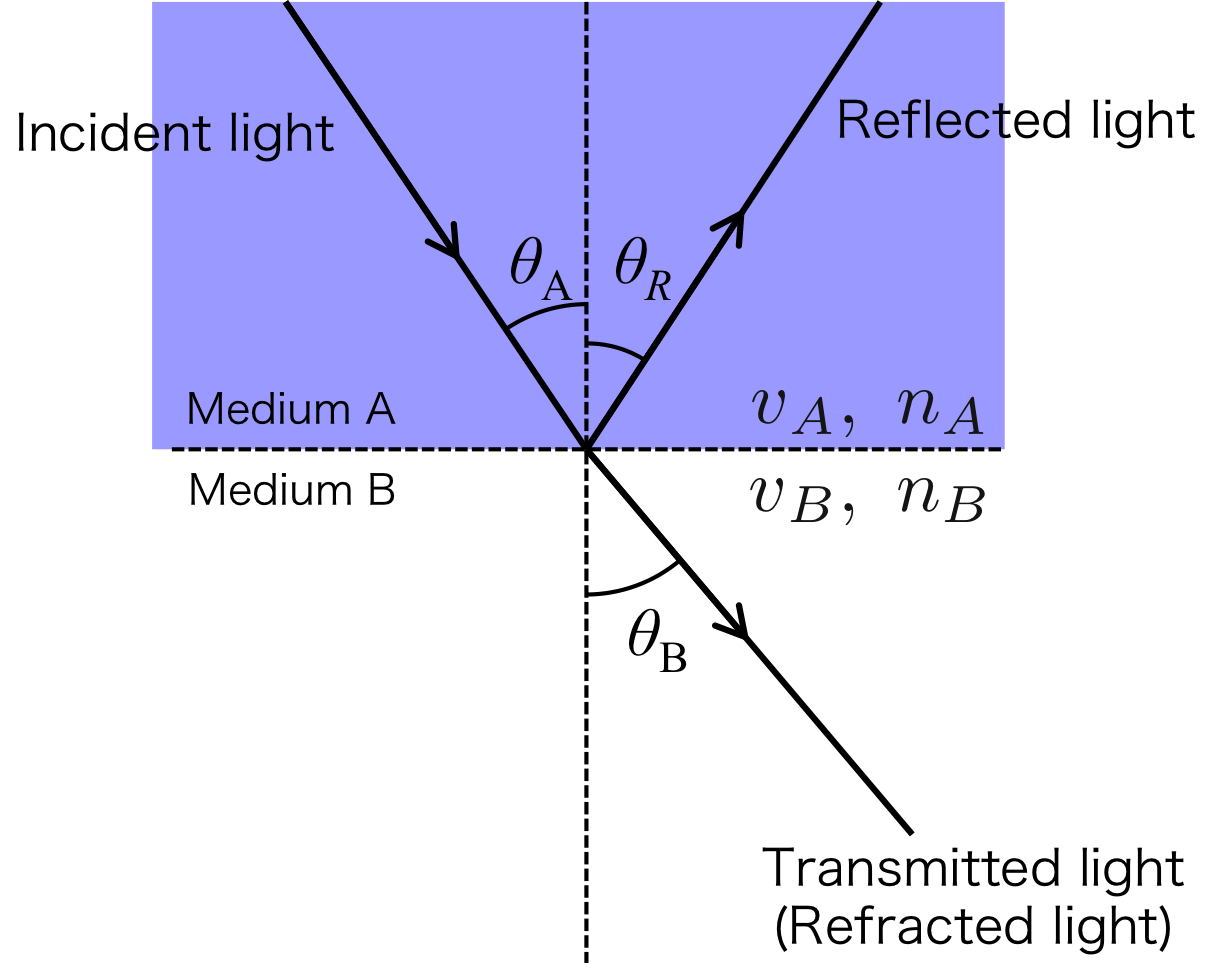
Figure 1. Reflection and Refraction of incident light

where \( \theta_A \), \( \theta_R \) and \( \theta_B \) are the incident, reflection, and refraction angles. The relationship between the incident and refraction angle is expressed by using the snell's law. \begin{eqnarray} n_A \sin \theta_A = n_B \sin \theta_B = Constant\ \ \ \ \ \ \ \ \ (1) \end{eqnarray} A part of the incident light becomes the refracted light while other part of it is reflected at the boundary surface. The incident angle \( \theta_A \) is equal to the reflection angle \( \theta_R \). According to equation 1, the refracted angle \( \theta_B \) increases along with an increase of the incident angle \( \theta_A \). Finally, the \( \theta_B \) becomes 90 degree as shown in Figure 2. The incident angle which makes the \( \theta_B \) to 90 degree is called "Critical angle".

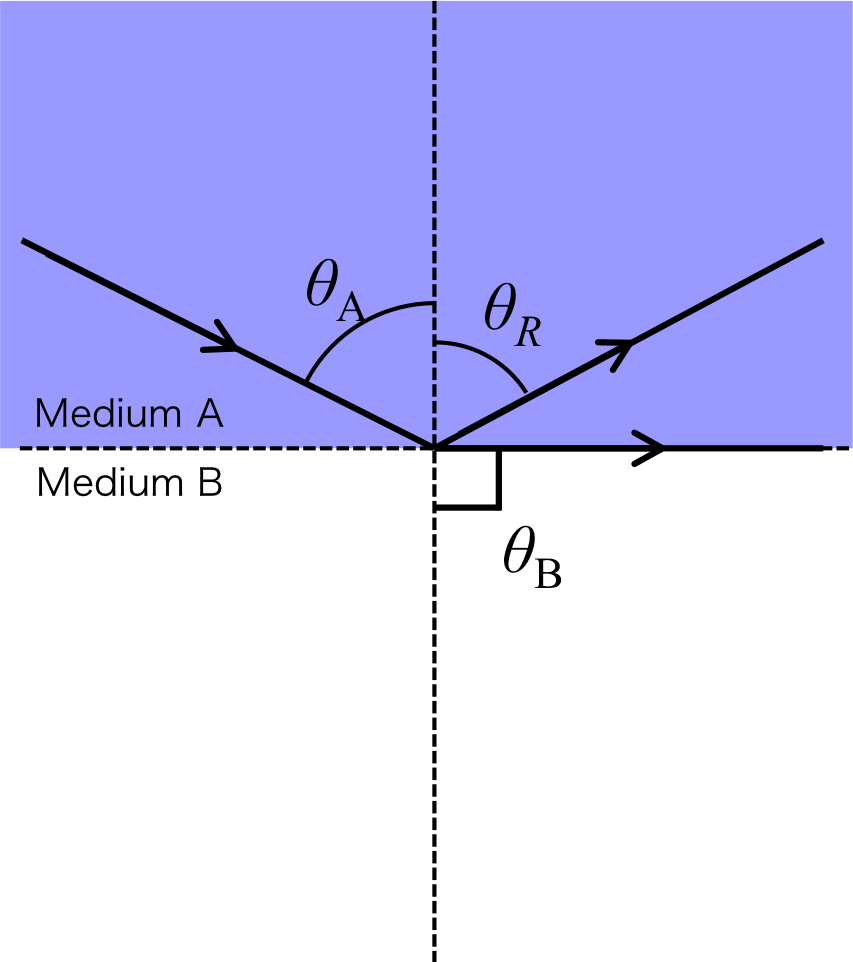
Figure 2. Critical angle

The refracted light cannot exist in the medium B when the incident angle becomes larger than the critical angle. Therefore, all of the incident light is reflected. This situation is called "Total reflection". The critical angle is derived from equation 1 as follows, \begin{eqnarray} \sin \theta_m = \frac{\sin \theta_m}{\sin 90^\circ} = \frac{n_B}{n_A} \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} If we know the refraction indices both mediums then we get the critical angle.

Sponsored Link