Coulomb’s potential (Coulomb’s energy)

Coulomb’s potential or Coulomb’s energy is the potential energy generated by the electrical force. Now, we consider a case in which the electric charge is moved from a point P to R. In this case, the reduced potential energy is equal to the work expressed as: \begin{eqnarray} W = - \int {\bf F} \cdot ds \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{eqnarray} If we assume that the potential energy at the point P and R are \( U_P \) and \( U_R \), then we obtain: \begin{eqnarray} U_P - U_R = W_{P\rightarrow R} = \int^R_P {\bf F} \cdot d{\bf s} = \int^{R}_{P} F_t ds \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) \end{eqnarray} \(F_t\) is the force in the direction along the infinitesimal changes \(ds\) of charge. That is,\( F_t = F cos \theta \).

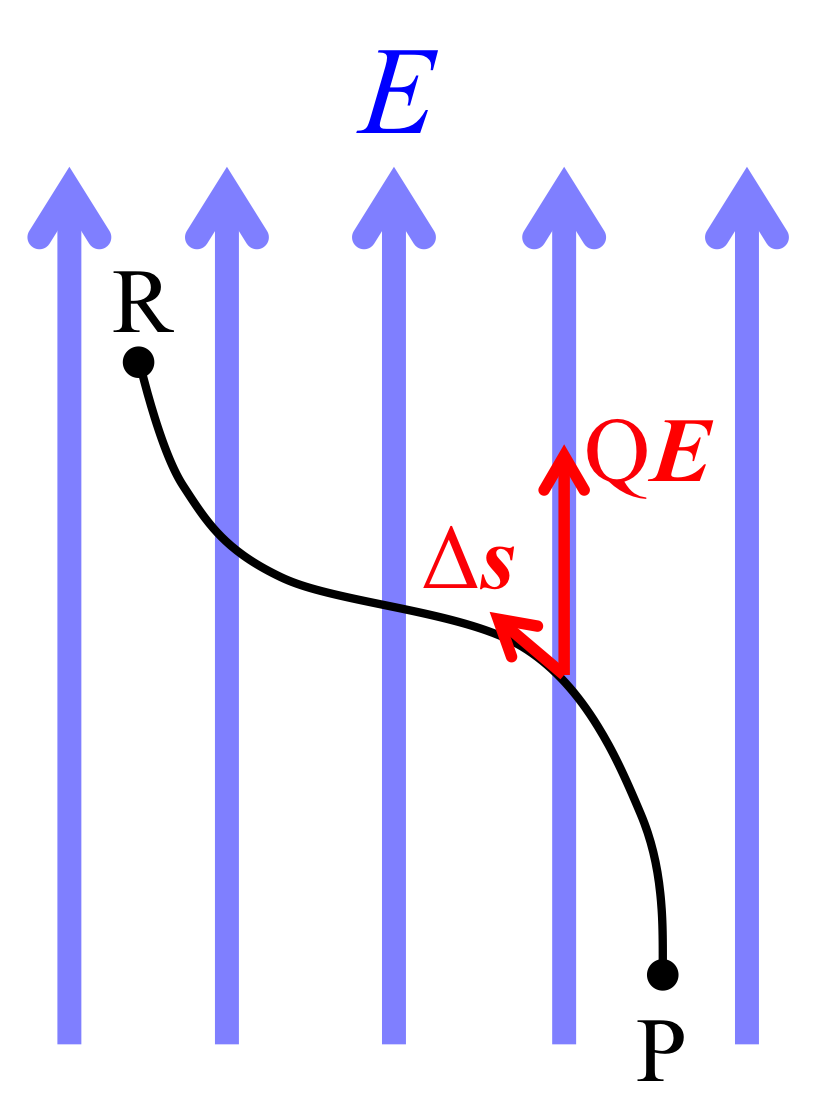
Figure 1. The path of the electric charge moving point from P to R with the electric field.

Figures 1 and 2 explain what \(ds\) is. \(W\) does not change regardless of the route that goes from the point P to the point R. In other words, \( W_{P\rightarrow R} \) is determined only by the positions of the start and end points. This property is a condition that can define the potential energy.

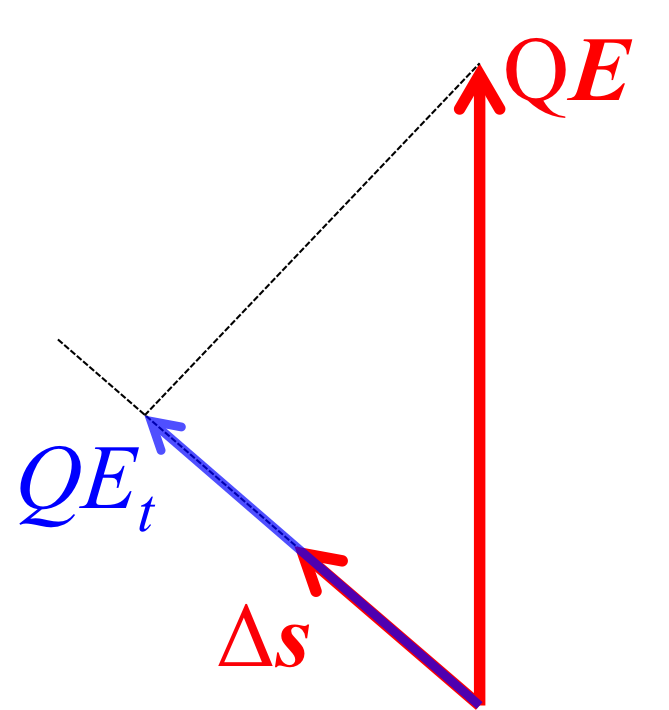
Figure 2. The force vector affecting the electric charge.

Here, we describe how to derive Coulomb’s potential. Now, we consider two charges \( Q_1 \) and \( Q_2 \). If we set the distance between \( Q_1 \) and \( Q_2 \) being \(r\), we obtain the force applied to these electric charges: \begin{eqnarray} F = \frac{Q_1 Q_2}{4 \pi \epsilon_0 r^2} \ \ \ \ \ \ \ \ \ \ (3) \end{eqnarray} The force generates a potential energy. We substitute Equation (3) to Equation (2), then: \begin{eqnarray} U(r_1) - U(r_2) = \int^{r_1}_{r_2} {\bf F} \cdot d{\bf s} = \frac{Q_1Q_2}{4 \pi \epsilon_0} \left( \frac{1}{r_1} - \frac{1}{r_2} \right) \ \ \ \ \ \ \ (4) \end{eqnarray} If we set \( r_1 = r\), \( r_2 = \infty \), we obtain Coulomb’s potential as follows: \begin{eqnarray} U(r) = \frac{Q_1Q_2}{4 \pi \epsilon_0 r} \end{eqnarray}

Sponsored link